Dijkstra算法、分层图最短路径

核心思想

Dijkstra算法

Dijkstra 算法：给定一个源点，求解从源点到每个点的最短路径长度。单源最短路径算法。 适用范围：有向图、边的权值没有负数

彻底暴力的 Dijkstra 算法，不讲、时间复杂度太差、无意义

普通堆实现的 Dijkstra 算法，最普遍、最常用 算法核心过程： 节点弹出过就忽略 节点没弹出过，让其它没弹出节点距离变小的记录加入堆

反向索引堆实现的 Dijkstra 算法，最快速、最极致 核心在于掌握反向索引堆

对应本节题目 1、题目 2、题目 3

普通版

普通堆实现的 Dijkstra 算法，时间复杂度 O (m * log m)，m 为边数

1、distance[i]表示从源点到 i 点的最短距离，visited[i]表示 i 节点是否从小根堆弹出过

2、准备好小根堆，小根堆存放记录：(x 点，源点到 x 的距离)，小根堆根据距离组织

3、令 distance[源点]=0，(源点，0) 进入小根堆

4、从小根堆弹出 (u 点，源点到 u 的距离)

a. 如果 visited[u] == true，不做任何处理，重复步骤 4

b. 如果 visited[u] == false，令 visited[u] = true，u 就算弹出过了 然后考察 u 的每一条边，假设某边去往 v，边权为 w

1）如果 visited[v] == false 并且 distance[u] + w < distance[v]

令 distance[v] = distance[u] + w，把 (v, distance[u] + w) 加入小根堆

2）处理完 u 的每一条边之后，重复步骤 4

5、小根堆为空过程结束，distance 表记录了源点到每个节点的最短距离。

模版代码

 class Solution {  
     public int networkDelayTime(int[][] times, int n, int k) {  
         //首先是建图  
         ArrayList<ArrayList<int[]>> graph=new ArrayList<>();  
         //初始化，注意测试用例给的数据都是从1开始的  
         for(int i=0;i<=n;i++){  
             graph.add(new ArrayList<>());  
         }  
         //添加对应的边  
         for(int[] time:times){  
             graph.get(time[0]).add(new int[]{time[1],time[2]});  
         }  
         //构造距离数组,注意测试用例是从1开始计数，从1到N  
         int[]distance=new int[n+1];  
         for(int i=1;i<=n;i++){  
             distance[i]=Integer.MAX_VALUE;  
         }  
         boolean[] visits=new boolean[n+1];  
         //准备普通的小根堆  
         PriorityQueue<int[]> heap=new PriorityQueue<>((a, b)->a[1]-b[1]);  
         //接下来开始Dijkstra算法  
         //初始化源点  
         distance[k]=0;  
         heap.add(new int[]{k,0});  
         while(!heap.isEmpty()){  
             int u=heap.poll()[0];  
             // 如果 visited[u] == true，不做任何处理，重复步骤 4            
             if(visits[u]){  
                 continue;  
             }  
             //如果 visited[u] == false，令 visited[u] = true，u 就算弹出过了  
             visits[k]=true;  
             //考察u的每一条边  
             for(int[]edge:graph.get(u)){  
                 //u->v  
                 int v=edge[0];  
                 //权重  
                 int w=edge[1];  
                 //如果 visited[v] == false 并且 distance[u] + w < distance[v]                
                 //令 distance[v] = distance[u] + w，把 (v, distance[u] + w) 加入小根堆  
                 if(distance[u]+w<distance[v]){  
                     distance[v]=distance[u]+w;  
                     heap.add(new int[]{v,distance[u]+w});  
                 }  
             }  
         }  
         int ans=0;  
         for(int i=1;i<=n;i++){  
             ans=Math.max(ans,distance[i]);  
         }  
         //若有无法到达的点则distance数组中必有一个代价为Integer.MAX_VALUE的点  
         return ans==Integer.MAX_VALUE?-1:ans;  
     }

优化版

反向索引堆实现的 Dijkstra 算法，时间复杂度 O (m * log n)，n 为节点数，m 为边数

1、准备好反向索引堆，根据源点到当前点的距离组织小根堆，可以做到如下操作

a. 新增记录 (x, 源点到 x 的距离)

b. 当源点到 x 的距离更新时，可以进行堆的调整

c. x 点一旦弹出，以后忽略 x

d. 弹出堆顶的记录 (u, 源点到 u 的距离)

2、把 (源点，0) 加入反向索引堆，过程开始

3、反向索引堆弹出 (u，源点到 u 的距离)，考察 u 的每一条边，假设某边去往 v，边权为 w

1）如果 v 没有进入过反向索引堆里，新增记录 (v, 源点到 u 的距离 + w)

2）如果 v 曾经从反向索引堆弹出过，忽略

3）如果 v 在反向索引堆里，看看源点到 v 的距离能不能变得更小，如果能，调整堆；不能，忽略

4）处理完 u 的每一条边，重复步骤 3

4 、反向索引堆为空过程结束。反向索引堆里记录了源点到每个节点的最短距离。

模版代码

 //Dijkstra算法优化版本：反向索引堆+链式前向星建图  
 class Solution2 {  
     public static int MAXN=101;  
     public static int MAXM=6001;  
     //链式前向星  
     public static int[]head=new int[MAXN];  
     public static int[]next=new int[MAXM];  
     public static int[]to=new int[MAXM];  
     public static int[]weight=new int[MAXM];  
     public static int cnt;  
     //反向索引堆  
     public static int[]heap=new int[MAXN];  
     // where[v] = -1，表示v这个节点，从来没有进入过堆  
     // where[v] = -2，表示v这个节点，已经弹出过了  
     // where[v] = i(>=0)，表示v这个节点，在堆上的i位置  
     public static int[]where=new int[MAXN];  
     public static int heapSize;  
     public static int[]distance=new int[MAXN];  
   
     public static int networkDelayTime(int[][] times, int n, int k) {  
         build(n);  
         //链式前向星建图  
         for(int[]edge:times){  
             addEdge(edge[0],edge[1],edge[2]);  
         }  
         //开始 Dijkstra算法  
         //源点进入  
         addOrUpdateOrIgnore(k,0);  
         while(!isEmpty()){  
             int u=pop();  
             for(int ei=head[u];ei>0;ei=next[ei]){  
                 addOrUpdateOrIgnore(to[ei],distance[u]+weight[ei]);  
             }  
         }  
         int ans=0;  
         for(int i=1;i<=n;i++){  
             ans=Math.max(ans,distance[i]);  
         }  
         return ans==Integer.MAX_VALUE?-1:ans;  
     }  
   
     public static void build(int n){  
         cnt=1;  
         heapSize=0;  
         Arrays.fill(head,0,n+1,0);  
         Arrays.fill(where,0,n+1,-1);  
         Arrays.fill(distance,0,n+1,Integer.MAX_VALUE);  
     }  
     public static void addEdge(int u,int v,int w){  
         next[cnt]=head[u];  
         to[cnt]=v;  
         weight[cnt]=w;  
         head[u]=cnt++;  
     }  
     //反向堆索引优化  
     /**  
      3，反向索引堆弹出 (u，源点到 u 的距离)，考察 u 的每一条边，假设某边去往 v，边权为 w  
      1）如果 v 没有进入过反向索引堆里，新增记录 (v, 源点到 u 的距离 + w)  
      2）如果 v 曾经从反向索引堆弹出过，忽略  
      3）如果 v 在反向索引堆里，看看源点到 v 的距离能不能变得更小，如果能，调整堆；不能，忽略  
      4）处理完 u 的每一条边，重复步骤 3  
      4 反向索引堆为空过程结束。反向索引堆里记录了源点到每个节点的最短距离。  
   
      */  
     public static void addOrUpdateOrIgnore(int v,int c){  
         if(where[v]==-1){  
             //将点加入堆中  
             heap[heapSize]=v;  
             where[v]=heapSize++;  
             distance[v]=c;  
             //新加入的点要网上看，使堆为小根堆  
             heapInsert(where[v]);  
         }else if(where[v]>=0){  
             distance[v]=Math.min(distance[v],c);  
             heapInsert(where[v]);  
         }  
     }  
   
     public static void heapInsert(int i){  
         while(distance[heap[i]]<distance[heap[(i-1)/2]]){  
             swap(i,(i-1)/2);  
             i=(i-1)/2;  
         }  
     }  
   
     public static boolean isEmpty(){  
         return heapSize==0;  
     }  
     public static int pop(){  
         int ans=heap[0];  
         //要复原小根堆  
         swap(0,--heapSize);  
         heapify(0);  
         //弹出后的点标记，后续有关这个点的所有操作都不再处理  
         where[ans]=-2;  
         return ans;  
     }  
   
     public static void heapify(int i){  
         int l=i*2+1;  
         while(l<heapSize){  
             int best=l+1<heapSize && distance[heap[l+1]]<distance[heap[l]]?l+1:l;  
             best=distance[heap[best]]<distance[heap[i]]?best:i;  
             if(best==i){  
                 break;  
             }  
             swap(i,best);  
             i=best;  
             l=2*i+1;  
         }  
     }  
   
     public static void swap(int i,int j){  
         //首先是堆中交换  
         int tmp=heap[i];  
         heap[i]=heap[j];  
         heap[j]=tmp;  
         //不要忘记索引数组的交换  
         where[heap[i]]=i;  
         where[heap[j]]=j;  
     }  
 }

分层图最短路

分层图最短路，又叫扩点最短路

不把实际位置看做图上的点，而是把实际位置及其状态的组合看做是图上的点，然后搜索 Bfs 或者 Dijkstra 的过程不变，只是扩了点（分层）而已 原理简单，核心在于如何扩点、如何到达、如何算距离，每个题可能都不一样

对应本节题目 4、题目 5、题目 6

例题

1、网络延迟时间

题目描述： 有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

示例 1：

输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 输出：2

示例 2：

输入：times = [[1,2,1]], n = 2, k = 1 输出：1

示例 3：

输入：times = [[1,2,1]], n = 2, k = 2 输出：-1

提示：

• 1 <= k <= n <= 100

• 1 <= times.length <= 6000

• times[i].length == 3

• 1 <= ui, vi <= n

• ui != vi

• 0 <= wi <= 100

• 所有 (ui, vi) 对都 互不相同（即，不含重复边）

Dijkstra 算法普通版：

 class Solution {  
     public int networkDelayTime(int[][] times, int n, int k) {  
         //首先是建图  
         ArrayList<ArrayList<int[]>> graph=new ArrayList<>();  
         //初始化，注意测试用例给的数据都是从1开始的  
         for(int i=0;i<=n;i++){  
             graph.add(new ArrayList<>());  
         }  
         //添加对应的边  
         for(int[] time:times){  
             graph.get(time[0]).add(new int[]{time[1],time[2]});  
         }  
         //构造距离数组,注意测试用例是从1开始计数，从1到N  
         int[]distance=new int[n+1];  
         for(int i=1;i<=n;i++){  
             distance[i]=Integer.MAX_VALUE;  
         }  
         boolean[] visits=new boolean[n+1];  
         //准备普通的小根堆  
         PriorityQueue<int[]> heap=new PriorityQueue<>((a, b)->a[1]-b[1]);  
         //接下来开始Dijkstra算法  
         //初始化源点  
         distance[k]=0;  
         heap.add(new int[]{k,0});  
         while(!heap.isEmpty()){  
             int u=heap.poll()[0];  
             // 如果 visited[u] == true，不做任何处理，重复步骤 4                  if(visits[u]){  
                 continue;  
             }  
             //如果 visited[u] == false，令 visited[u] = true，u 就算弹出过了  
             visits[k]=true;  
             //考察u的每一条边  
             for(int[]edge:graph.get(u)){  
                 //u->v  
                 int v=edge[0];  
                 //权重  
                 int w=edge[1];  
                 //如果 visited[v] == false 并且 distance[u] + w < distance[v]                //令 distance[v] = distance[u] + w，把 (v, distance[u] + w) 加入小根堆  
                 if(distance[u]+w<distance[v]){  
                     distance[v]=distance[u]+w;  
                     heap.add(new int[]{v,distance[u]+w});  
                 }  
             }  
         }  
         int ans=0;  
         for(int i=1;i<=n;i++){  
             ans=Math.max(ans,distance[i]);  
         }  
         //若有无法到达的点则distance数组中必有一个代价为Integer.MAX_VALUE的点  
         return ans==Integer.MAX_VALUE?-1:ans;  
     }

Dijkstra 算法优化版

   //Dijkstra算法优化版本：反向索引堆+链式前向星建图  
 class Solution2 {  
     public static int MAXN=101;  
     public static int MAXM=6001;  
     //链式前向星  
     public static int[]head=new int[MAXN];  
     public static int[]next=new int[MAXM];  
     public static int[]to=new int[MAXM];  
     public static int[]weight=new int[MAXM];  
     public static int cnt;  
     //反向索引堆  
     public static int[]heap=new int[MAXN];  
     // where[v] = -1，表示v这个节点，从来没有进入过堆  
     // where[v] = -2，表示v这个节点，已经弹出过了  
     // where[v] = i(>=0)，表示v这个节点，在堆上的i位置  
     public static int[]where=new int[MAXN];  
     public static int heapSize;  
     public static int[]distance=new int[MAXN];  
   
     public static int networkDelayTime(int[][] times, int n, int k) {  
         build(n);  
         //链式前向星建图  
         for(int[]edge:times){  
             addEdge(edge[0],edge[1],edge[2]);  
         }  
         //开始 Dijkstra算法  
         //源点进入  
         addOrUpdateOrIgnore(k,0);  
         while(!isEmpty()){  
             int u=pop();  
             for(int ei=head[u];ei>0;ei=next[ei]){  
                 addOrUpdateOrIgnore(to[ei],distance[u]+weight[ei]);  
             }  
         }  
         int ans=0;  
         for(int i=1;i<=n;i++){  
             ans=Math.max(ans,distance[i]);  
         }  
         return ans==Integer.MAX_VALUE?-1:ans;  
     }  
   
     public static void build(int n){  
         cnt=1;  
         heapSize=0;  
         Arrays.fill(head,0,n+1,0);  
         Arrays.fill(where,0,n+1,-1);  
         Arrays.fill(distance,0,n+1,Integer.MAX_VALUE);  
     }  
     public static void addEdge(int u,int v,int w){  
         next[cnt]=head[u];  
         to[cnt]=v;  
         weight[cnt]=w;  
         head[u]=cnt++;  
     }  
     //反向堆索引优化  
     /**  
      3，反向索引堆弹出 (u，源点到 u 的距离)，考察 u 的每一条边，假设某边去往 v，边权为 w  
      1）如果 v 没有进入过反向索引堆里，新增记录 (v, 源点到 u 的距离 + w)  
      2）如果 v 曾经从反向索引堆弹出过，忽略  
      3）如果 v 在反向索引堆里，看看源点到 v 的距离能不能变得更小，如果能，调整堆；不能，忽略  
      4）处理完 u 的每一条边，重复步骤 3  
      4 反向索引堆为空过程结束。反向索引堆里记录了源点到每个节点的最短距离。  
   
      */  
     public static void addOrUpdateOrIgnore(int v,int c){  
         if(where[v]==-1){  
             //将点加入堆中  
             heap[heapSize]=v;  
             where[v]=heapSize++;  
             distance[v]=c;  
             //新加入的点要网上看，使堆为小根堆  
             heapInsert(where[v]);  
         }else if(where[v]>=0){  
             distance[v]=Math.min(distance[v],c);  
             heapInsert(where[v]);  
         }  
     }  
   
     public static void heapInsert(int i){  
         while(distance[heap[i]]<distance[heap[(i-1)/2]]){  
             swap(i,(i-1)/2);  
             i=(i-1)/2;  
         }  
     }  
   
     public static boolean isEmpty(){  
         return heapSize==0;  
     }  
     public static int pop(){  
         int ans=heap[0];  
         //要复原小根堆  
         swap(0,--heapSize);  
         heapify(0);  
         //弹出后的点标记，后续有关这个点的所有操作都不再处理  
         where[ans]=-2;  
         return ans;  
     }  
   
     public static void heapify(int i){  
         int l=i*2+1;  
         while(l<heapSize){  
             int best=l+1<heapSize && distance[heap[l+1]]<distance[heap[l]]?l+1:l;  
             best=distance[heap[best]]<distance[heap[i]]?best:i;  
             if(best==i){  
                 break;  
             }  
             swap(i,best);  
             i=best;  
             l=2*i+1;  
         }  
     }  
   
     public static void swap(int i,int j){  
         //首先是堆中交换  
         int tmp=heap[i];  
         heap[i]=heap[j];  
         heap[j]=tmp;  
         //不要忘记索引数组的交换  
         where[heap[i]]=i;  
         where[heap[j]]=j;  
     }  
 }

2、最小体力消耗路径

题目描述： 你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

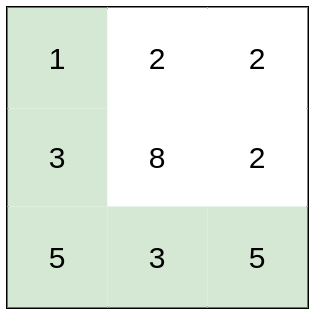
输入：heights = [[1,2,2],[3,8,2],[5,3,5]] 输出：2 解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。 这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

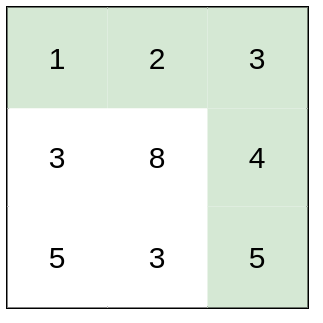
输入：heights = [[1,2,3],[3,8,4],[5,3,5]] 输出：1 解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

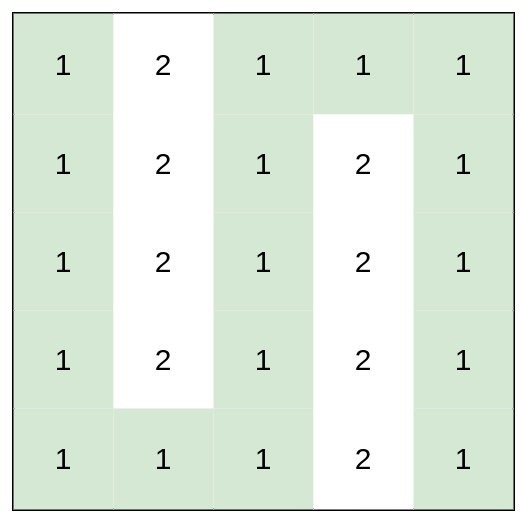
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]] 输出：0 解释：上图所示路径不需要消耗任何体力。

提示：

• rows == heights.length

• columns == heights[i].length

• 1 <= rows, columns <= 100

• 1 <= heights[i][j] <= 106

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code02_PathWithMinimumEffort  
  * @description: 最小体力消耗路径  
  * // 你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights  
  * // 其中 heights[row][col] 表示格子 (row, col) 的高度  
  * // 一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1)  
  * // （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动  
  * // 你想要找到耗费 体力 最小的一条路径  
  * // 一条路径耗费的体力值是路径上，相邻格子之间高度差绝对值的最大值  
  * // 请你返回从左上角走到右下角的最小 体力消耗值  
  * // 测试链接 ：https://leetcode.cn/problems/path-with-minimum-effort/  
  * @author: zs宝  
  * @create: 2025-07-23 11:03  
  * @Version 1.0  
  **/  
 package main.java.class064;  
   
 import java.util.PriorityQueue;  
   
 public class Code02_PathWithMinimumEffort {  
     class Solution {  
         public int minimumEffortPath(int[][] heights) {  
             int[]move=new int[]{-1,0,1,0,-1};  
             int n=heights.length;  
             int m=heights[0].length;  
             boolean[][]visited=new boolean[n][m];  
             int[][]distance=new int[n][m];  
             for(int i=0;i<n;i++){  
                 for(int j=0;j<m;j++){  
                     distance[i][j]=Integer.MAX_VALUE;  
                 }  
             }  
             distance[0][0]=0;  
             //0：x  
             //1：y  
             //2: distance            
             PriorityQueue<int[]> heap=new PriorityQueue<>((a, b)->a[2]-b[2]);  
             heap.add(new int[]{0,0,distance[0][0]});  
             while(!heap.isEmpty()){  
                 int[]record=heap.poll();  
                 int x=record[0];  
                 int y=record[1];  
                 int w=record[2];  
                 if(visited[x][y]){  
                     continue;  
                 }  
                 if(x==n-1 && y==m-1){  
                     return w;  
                 }  
                 visited[x][y]=true;  
                 //开始向四周扩散  
                 for(int i=0,nx,ny,nw;i<4;i++){  
                     nx=x+move[i];  
                     ny=y+move[i+1];  
                     if(nx>=0 && nx<n && ny>=0 && ny<m && !visited[nx][ny]){  
                         nw=Math.max(w,Math.abs(heights[x][y]-heights[nx][ny]));  
                         if(nw<distance[nx][ny]){  
                             distance[nx][ny]=nw;  
                             heap.add(new int[]{nx,ny,nw});  
                         }  
   
                     }  
                 }  
             }  
             return -1;  
         }  
     }  
 }

3、水位上升的泳池中游泳

题目描述： 在一个 n x n 的整数矩阵 grid 中，每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。

当开始下雨时，在时间为 t 时，水池中的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的。当然，在你游泳的时候你必须待在坐标方格里面。

你从坐标方格的左上平台 (0，0) 出发。返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间 。

示例 1:

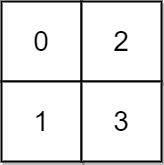
输入: grid = [[0,2],[1,3]] 输出: 3 解释: 时间为0时，你位于坐标方格的位置为 (0, 0)。 此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。 等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置

示例 2:

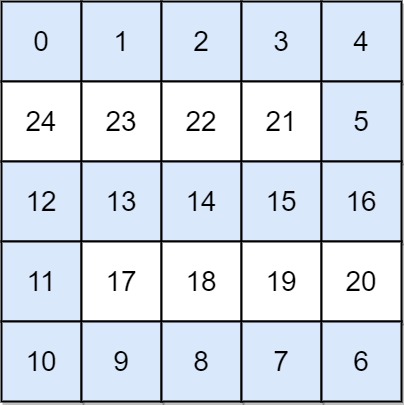
输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]] 输出: 16 解释: 最终的路线用加粗进行了标记。 我们必须等到时间为 16，此时才能保证平台 (0, 0) 和 (4, 4) 是连通的

提示:

• n == grid.length

• n == grid[i].length

• 1 <= n <= 50

• 0 <= grid[i][j] < n2

• grid[i][j] 中每个值 均无重复

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code03_SwimInRisingWater  
  * @description: 水位上升的泳池中游泳  
  * // 在一个 n x n 的整数矩阵 grid 中  
  * // 每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度  
  * // 当开始下雨时，在时间为 t 时，水池中的水位为 t  
  * // 你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台  
  * // 假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的  
  * // 当然，在你游泳的时候你必须待在坐标方格里面。  
  * // 你从坐标方格的左上平台 (0，0) 出发  
  * // 返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间  
  * // 测试链接 : https://leetcode.cn/problems/swim-in-rising-water/  
  * @author: zs宝  
  * @create: 2025-07-24 09:29  
  * @Version 1.0  
  **/  
 package main.java.class064;  
   
 import java.util.PriorityQueue;  
   
 public class Code03_SwimInRisingWater {  
     class Solution {  
         public int swimInWater(int[][] grid) {  
             int[]move=new int[]{-1,0,1,0,-1};  
             int n=grid.length;  
             int[][]distance=new int[n][n];  
             for(int i=0;i<n;i++){  
                 for(int j=0;j<n;j++){  
                     distance[i][j]=Integer.MAX_VALUE;  
                 }  
             }  
             boolean[][]visited=new boolean[n][n];  
             PriorityQueue<int[]> heap=new PriorityQueue<>((a, b)->a[2]-b[2]);  
             //开始Dijkstra算法  
             distance[0][0]=grid[0][0];  
             heap.add(new int[]{0,0,distance[0][0]});  
             while(!heap.isEmpty()){  
                 int[]record=heap.poll();  
                 int x=record[0];  
                 int y=record[1];  
                 int w=record[2];  
                 if(visited[x][y]){  
                     continue;  
                 }  
                 if(x==n-1 && y==n-1){  
                     return w;  
                 }  
                 visited[x][y]=true;  
                 for(int i=0,nx,ny,nw;i<4;i++){  
                     nx=x+move[i];  
                     ny=y+move[i+1];  
                     if(nx>=0 && nx<n && ny>=0 && ny<n && !visited[nx][ny]){  
                         nw=Math.max(w,grid[nx][ny]);  
                         if(nw<distance[nx][ny]){  
                             distance[nx][ny]=nw;  
                             heap.add(new int[]{nx,ny,distance[nx][ny]});  
                         }  
                     }  
                 }  
             }  
             return -1;  
         }  
     }  
 }

4、获取所有钥匙的最短路径

题目描述： 给定一个二维网格 grid ，其中：

• '.' 代表一个空房间

• '#' 代表一堵墙

• '@' 是起点

• 小写字母代表钥匙

• 大写字母代表锁

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 k 为 钥匙/锁 的个数，且满足 1 <= k <= 6，字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1 。

示例 1：

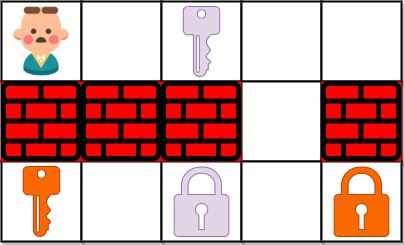
输入：grid = ["@.a..","###.#","b.A.B"] 输出：8 解释：目标是获得所有钥匙，而不是打开所有锁。

示例 2：

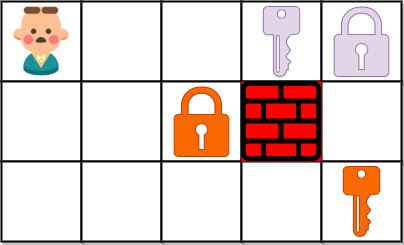
输入：grid = ["@..aA","..B#.","....b"] 输出：6

示例 3:

输入: grid = ["@Aa"] 输出: -1

提示：

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 30

• grid[i][j] 只含有 '.', '#', '@', 'a'-``'f``' 以及 'A'-'F'

• 钥匙的数目范围是 [1, 6] 

• 每个钥匙都对应一个 不同 的字母

• 每个钥匙正好打开一个对应的锁

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code04_ShortestPathToGetAllKeys  
  * @description:获取所有钥匙的最短路径  
  * // 给定一个二维网格grid，其中：  
  * // '.' 代表一个空房间、'#' 代表一堵、'@'是起点  
  * // 小写字母代表钥匙、大写字母代表锁  
  * // 从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间  
  * // 不能在网格外面行走，也无法穿过一堵墙  
  * // 如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。  
  * // 假设 k为 钥匙/锁 的个数，且满足1 <= k<= 6，  
  * // 字母表中的前 k个字母在网格中都有自己对应的一个小写和一个大写字母  
  * // 换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁  
  * // 另外，代表钥匙和锁的字母互为大小写并按字母顺序排列  
  * // 返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回-1。  
  * // 测试链接：https://leetcode.cn/problems/shortest-path-to-get-all-keys  
  * @author: zs宝  
  * @create: 2025-07-24 10:02  
  * @Version 1.0  
  **/  
 package main.java.class064;  
   
 public class Code04_ShortestPathToGetAllKeys {  
     class Solution {  
         public static int MAXM=31;  
         public static int MAXN=31;  
         public static int MAXK=6;  
         //图的网格  
         public static char[][] grid=new char[MAXM][];  
         //是否经过某个点的某个状态  
         public static boolean[][][]visited=new boolean[MAXM][MAXN][1<<MAXK];  
         //队列  
         //0：x  
         //1: y        //2: 当前的状态（身上的有哪些钥匙）  
         public static int[][]queue=new int[MAXM*MAXN*(1<<MAXK)][3];  
         public static int l,r,n,m,key;  
         public static int[]move=new int[]{-1,0,1,0,-1};  
         public int shortestPathAllKeys(String[] g) {  
             build(g);  
             int level=1;  
             //bfs  
             while(l<r){  
                 int size=r-l;  
                 for(int k=0,x,y,s;k<size;k++){  
                     //当前状态  
                     x=queue[l][0];  
                     y=queue[l][1];  
                     s=queue[l++][2];  
                     //向四周寻找  
                     for(int i=0,nx,ny,ns;i<4;i++){  
                         nx=x+move[i];  
                         ny=y+move[i+1];  
                         ns=s;  
                         //如果越界或者撞到了墙上，则此路不通  
                         if(nx<0 || nx>=m || ny<0 || ny>=n || grid[nx][ny]=='#'){  
                             continue;  
                         }  
                         //如果遇到了锁，但是身上并没有其钥匙，那么此路不通  
                         if(grid[nx][ny]>='A' && grid[nx][ny]<='F' && (ns&(1<<(grid[nx][ny]-'A')))==0){  
                             continue;  
                         }  
                         //如果遇到一把钥匙,则收集  
                         if(grid[nx][ny]>='a' && grid[nx][ny]<='f'){  
                             ns|=(1<<(grid[nx][ny]-'a'));  
                         }  
                         //如果钥匙收集全了，则直接返回结果，一个剪枝步骤  
                         if(ns==key){  
                             return level;  
                         }  
                         //如果当前点状态未被参观，则加入参观，同时将其近期如队列  
                         if(!visited[nx][ny][ns]){  
                             visited[nx][ny][ns]=true;  
                             queue[r][0]=nx;  
                             queue[r][1]=ny;  
                             queue[r++][2]=ns;  
                         }  
                     }  
                 }  
                 level++;  
             }  
             return -1;  
         }  
         public static void build(String[]g){  
             //首先将字符数组转换为char的网格二维数组  
             m=g.length;  
             n=g[0].length();  
             for(int i=0;i<m;i++){  
                 grid[i]=g[i].toCharArray();  
             }  
             l=r=key=0;  
             //找到初始位置出发点、钥匙收集全的状态  
             for(int i=0;i<m;i++){  
                 for(int j=0;j<n;j++){  
                     //找到初始位置  
                     if(grid[i][j]=='@'){  
                         queue[r][0]=i;  
                         queue[r][1]=j;  
                         queue[r++][2]=0;  
                     }  
                     //收集钥匙的状态  
                     if(grid[i][j]>='a' && grid[i][j]<='f'){  
                         key|=1<<(grid[i][j]-'a');  
                     }  
                 }  
             }  
             //visited数组的遍历状态  
             for(int i=0;i<m;i++){  
                 for(int j=0;j<n;j++){  
                     for(int s=0;s<=key;s++){  
                         visited[i][j][s]=false;  
                     }  
                 }  
             }  
         }  
     }  
 }

5、电动车游城市

题目描述： 小明的电动车电量充满时可行驶距离为 cnt，每行驶 1 单位距离消耗 1 单位电量，且花费 1 单位时间。小明想选择电动车作为代步工具。地图上共有 N 个景点，景点编号为 0 ~ N-1。他将地图信息以 [城市 A 编号,城市 B 编号,两城市间距离] 格式整理在在二维数组 paths，表示城市 A、B 间存在双向通路。初始状态，电动车电量为 0。每个城市都设有充电桩，charge[i] 表示第 i 个城市每充 1 单位电量需要花费的单位时间。请返回小明最少需要花费多少单位时间从起点城市 start 抵达终点城市 end。

示例 1：

输入：paths = [[1,3,3],[3,2,1],[2,1,3],[0,1,4],[3,0,5]], cnt = 6, start = 1, end = 0, charge = [2,10,4,1] 输出：43 解释：最佳路线为：1->3->0。 在城市 1 仅充 3 单位电至城市 3，然后在城市 3 充 5 单位电，行驶至城市 0。 充电用时共 310 + 51= 35 行驶用时 3 + 5 = 8，此时总用时最短 43。

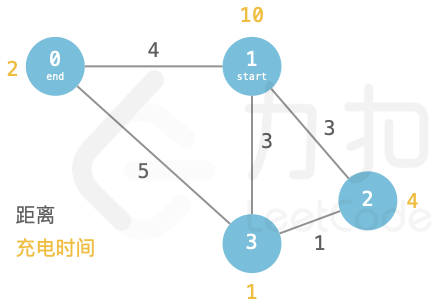
示例 2：

输入：paths = [[0,4,2],[4,3,5],[3,0,5],[0,1,5],[3,2,4],[1,2,8]], cnt = 8, start = 0, end = 2, charge = [4,1,1,3,2] 输出：38 解释：最佳路线为：0->4->3->2。 城市 0 充电 2 单位，行驶至城市 4 充电 8 单位，行驶至城市 3 充电 1 单位，最终行驶至城市 2。 充电用时 42+28+3*1 = 27 行驶用时 2+5+4 = 11，总用时最短 38。

提示：

• 1 <= paths.length <= 200

• paths[i].length == 3

• 2 <= charge.length == n <= 100

• 0 <= path[i][0],path[i][1],start,end < n

• 1 <= cnt <= 100

• 1 <= path[i][2] <= cnt

• 1 <= charge[i] <= 100

• 题目保证所有城市相互可以到达

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code05_VisitCityMinCost  
  * @description: 电动车游城市  
  * // 小明的电动车电量充满时可行驶距离为 cnt，每行驶 1 单位距离消耗 1 单位电量，且花费 1 单位时间  
  * // 小明想选择电动车作为代步工具。地图上共有 N 个景点，景点编号为 0 ~ N-1  
  * // 他将地图信息以 [城市 A 编号,城市 B 编号,两城市间距离] 格式整理在在二维数组 paths，  
  * // 表示城市 A、B 间存在双向通路。  
  * // 初始状态，电动车电量为 0。每个城市都设有充电桩，  
  * // charge[i] 表示第 i 个城市每充 1 单位电量需要花费的单位时间。  
  * // 请返回小明最少需要花费多少单位时间从起点城市 start 抵达终点城市 end  
  * // 测试链接 : https://leetcode.cn/problems/DFPeFJ/  
  * @author: zs宝  
  * @create: 2025-07-24 11:24  
  * @Version 1.0  
  **/  
 package main.java.class064;  
   
 import java.util.ArrayList;  
 import java.util.PriorityQueue;  
   
 public class Code05_VisitCityMinCost {  
     class Solution {  
         public int electricCarPlan(int[][] paths, int cnt, int start, int end, int[] charge) {  
             int n=charge.length;  
             //建图  
             ArrayList<ArrayList<int[]>>graph=new ArrayList<>();  
             for(int i=0;i<n;i++){  
                 graph.add(new ArrayList<>());  
             }  
             for(int[] path:paths){  
                 //注意是无向图  
                 graph.get(path[0]).add(new int[]{path[1],path[2]});  
                 graph.get(path[1]).add(new int[]{path[0],path[2]});  
             }  
             //距离数组  
             //这里的距离是代价，由于每个城市对应的电动车的电量可以有cnt种  
             //因此这里每个点指的不再是城市或者道路节点，而是到达某个城市时自身拥有的一个状态为一个点（电动车电量）  
             //由于电量是1-cnt因此数组要有cnt+1个才能对应装  
             int[][]distance=new int[n][cnt+1];  
             for(int i=0;i<n;i++){  
                 for(int j=0;j<=cnt;j++){  
                     distance[i][j]=Integer.MAX_VALUE;  
                 }  
             }  
             //构建参观数组  
             boolean [][]visited=new boolean[n][cnt+1];  
             //由于题目本质还是找花费最小代价的最短路径问题，且题目边的权重不同，因此用Dijkstra算法  
             //0:城市点；1：电量；2：代价  
             PriorityQueue<int[]> heap=new PriorityQueue<>((a, b)->a[2]-b[2]);  
             //由于初始状态电动车无电  
             distance[start][0]=0;  
             heap.add(new int[]{start,0,distance[start][0]});  
             while(!heap.isEmpty()){  
                 int[]record=heap.poll();  
                 //当前城市  
                 int cur=record[0];  
                 //当前电量  
                 int power=record[1];  
                 //代价  
                 int cost=record[2];  
                 if(visited[cur][power]){  
                     continue;  
                 }  
                 if(cur==end){  
                     return cost;  
                 }  
                 visited[cur][power]=true;  
                 //接下来就是这个题目的关键，这也是分层最短路径与普通的寻找最短路径最大的区别，本身带有太多状态的考量  
                 //当前点充电否，是不充电直接开往下一个城市，还是充电开往下一个城市，充电充多少  
   
                 //如果充电,我们每次充一格点加入heap小根堆，后续每次弹出都会再充一格点直到状态遍历完  
                 if(power+1<=cnt && !visited[cur][power+1]){  
                     if(cost+charge[cur]<distance[cur][power+1]){  
                         distance[cur][power+1]=cost+charge[cur];  
                         heap.add(new int[]{cur,power+1,distance[cur][power+1]});  
                     }  
                 }  
                 //不充电直接开往下一个城市  
                 for(int[]path:graph.get(cur)){  
                     int nextCity=path[0];  
                     int nextPower=power-path[1];  
                     int nextCost=cost+path[1];  
                     if(nextPower>=0 && !visited[nextCity][nextPower]&& nextCost < distance[nextCity][nextPower]){  
                         heap.add(new int[]{nextCity,nextPower,nextCost});  
                     }  
                 }  
             }  
             return -1;  
         }  
     }  
 }

6、飞行路线

题目描述

Alice 和 Bob 现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 n 个城市设有业务，设这些城市分别标记为 0 到 n-1，一共有 m 种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 k 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少？ 输入格式

第一行三个整数 n,m,k，分别表示城市数，航线数和免费乘坐次数。

接下来一行两个整数 s,t，分别表示他们出行的起点城市编号和终点城市编号。

接下来 m 行，每行三个整数 a,b,c，表示存在一种航线，能从城市 a 到达城市 b，或从城市 b 到达城市 a，价格为 c。

输出格式

输出一行一个整数，为最少花费。

输入输出样例

输入

5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100

输出

8

说明/提示

数据规模与约定

对于 30\% 的数据，2 \le n \le 50，1 \le m \le 300，k=0。

对于 50\% 的数据，2 \le n \le 600，1 \le m \le 6\times10^3，0 \le k \le 1。

对于 100\% 的数据，2 \le n \le 10^4，1 \le m \le 5\times 10^4，0 \le k \le 10，0\le s,t,a,b < n，a\ne b，0\le c\le 10^3。

另外存在一组 hack 数据。

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code06_FlightPath1  
  * @description:飞行路线（语言提供的堆）  
  * // Alice和Bob现在要乘飞机旅行，他们选择了一家相对便宜的航空公司  
  * // 该航空公司一共在n个城市设有业务，设这些城市分别标记为0 ~ n−1  
  * // 一共有m种航线，每种航线连接两个城市，并且航线有一定的价格  
  * // Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机  
  * // 航空公司对他们这次旅行也推出优惠，他们可以免费在最多k种航线上搭乘飞机  
  * // 那么 Alice 和 Bob 这次出行最少花费多少  
  * // 测试链接 : https://www.luogu.com.cn/problem/P4568  
  * @author: zs宝  
  * @create: 2025-07-25 10:45  
  * @Version 1.0  
  **/  
 package main.java.class064;  
   
 import java.io.*;  
 import java.util.Arrays;  
   
 public class Code06_FlightPath {  
     public static int MAXN=10001;  
     //注意无向图，最大的边数*2  
     public static int MAXM=100001;  
     public static int MAXK=11;  
     public static int n,m,k,start,end;  
     //建图的链式前向星  
     public static int[]head=new int[MAXN];  
     public static int[]next=new int[MAXM];  
     public static int[]to=new int[MAXM];  
     public static int[]weight=new int[MAXM];  
     public static int cnt;  
   
     //代价数组  
     //在某个城市乘坐了第几次免费航线，当前的代价是多少  
     //这里的点是城市+乘坐免费航线次数的组合  
     public static int[][]distance=new int[MAXN][MAXK];  
     public static boolean[][] visited = new boolean[MAXN][MAXK];  
     //Dijkstra算法的小根堆  
     //自己写的堆优化  
     public static int[][]heap=new int[MAXN*MAXK][3];  
     public static int heapSize;  
   
     public static void main(String[] args) throws IOException {  
         BufferedReader bufferedReader=new BufferedReader(new InputStreamReader(System.in));  
         StreamTokenizer in=new StreamTokenizer(bufferedReader);  
         PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));  
         while (in.nextToken()!=StreamTokenizer.TT_EOF){  
             n=(int)in.nval;  
             in.nextToken();  
             m=(int)in.nval;  
             in.nextToken();  
             k=(int)in.nval;  
             in.nextToken();  
             start=(int)in.nval;  
             in.nextToken();  
             end=(int)in.nval;  
             build();  
             for(int i=0,a,b,c;i<m;i++){  
                 in.nextToken();  
                 a=(int)in.nval;  
                 in.nextToken();  
                 b=(int)in.nval;  
                 in.nextToken();  
                 c=(int)in.nval;  
                 addEdge(a,b,c);  
                 addEdge(b,a,c);  
             }  
              out.println(dijkstra());  
         }  
         out.flush();  
         out.close();  
         bufferedReader.close();  
     }  
     public static void build(){  
         //链式前向星初始化  
         cnt=1;  
         Arrays.fill(head,0,n+1,0);  
         //距离数组初始化  
         for(int i=0;i<n;i++){  
             for(int j=0;j<=k;j++){  
                 distance[i][j]=Integer.MAX_VALUE;  
                 visited[i][j]=false;  
             }  
         }  
         //堆初始化  
         heapSize=0;  
   
     }  
     //链式前向星加边  
     public static void addEdge(int u,int v,int w){  
         next[cnt]=head[u];  
         to[cnt]=v;  
         weight[cnt]=w;  
         head[u]=cnt++;  
     }  
     //用来代表小根堆每次弹出的节点中的数据  
     public static int cur,use,cost;  
     public static int dijkstra(){  
         distance[start][0]=0;  
         //小根堆加入  
         push(start,0,0);  
         while(!isEmpty()){  
             //弹出小根堆根节点  
             pop();  
             if(visited[cur][use]){  
                 continue;  
             }  
             if(cur==end){  
                 return cost;  
             }  
             visited[cur][use]=true;  
             //对于下一段航线，分别尝试使用免费和不适用免费  
             for(int ei=head[cur];ei>0;ei=next[ei]){  
                 int next = to[ei];  
                 int w=weight[ei];  
                 //使用免费  
                 if(use<k && !visited[next][use+1] && distance[cur][use]<distance[next][use+1]){  
                     distance[next][use+1]=distance[cur][use];  
                     push(next,use+1,distance[next][use+1]);  
                 }  
                 //不使用免费  
                 if(!visited[next][use] && distance[cur][use]+w<distance[next][use]){  
                     distance[next][use]=distance[cur][use]+w;  
                     push(next,use,distance[next][use]);  
                 }  
             }  
         }  
         return -1;  
     }  
   
     public static void push(int u,int t,int c){  
         heap[heapSize][0]=u;  
         heap[heapSize][1]=t;  
         heap[heapSize][2]=c;  
         heapInsert(heapSize++);  
     }  
     public static void heapInsert(int i){  
         while (i>0 && heap[i][2]<heap[(i-1)/2][2]){  
             swap(i,(i-1)/2);  
             i=(i-1)/2;  
         }  
     }  
     public static void swap(int i,int j){  
         int[]temp=heap[i];  
         heap[i]=heap[j];  
         heap[j]=temp;  
     }  
   
     public static void pop(){  
         cur=heap[0][0];  
         use=heap[0][1];  
         cost=heap[0][2];  
         swap(0,--heapSize);  
         heapfy(0);  
     }  
     public static void heapfy(int i){  
         int l=2*i+1;  
         while (l<heapSize){  
             int best=(l+1)<heapSize && heap[l+1][2]<heap[l][2]?l+1:l;  
             best=heap[best][2]<heap[i][2]?best:i;  
             if(best==i){  
                 break;  
             }  
             swap(best,i);  
             i=best;  
             l=2*i+1;  
         }  
     }  
   
     public static boolean isEmpty(){  
         return heapSize==0;  
     }  
   
 }

参考资料

• 左程云-算法通关系列