上一节的我们更多是从暴力递归一步一步变为动态规划，本节我们尝试直接从动态规划入手。
例题
1、不同的子序列
题目描述： 给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数。
测试用例保证结果在 32 位有符号整数范围内。
示例 1：
输入：s = "rabbbit", t = "rabbit" **输出**：3 解释： 如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。 **rabb**b**it** **ra**b**bbit** **rab**b**bit**
示例 2：
输入：s = "babgbag", t = "bag" **输出**：5 解释： 如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 **ba**b**g**bag **ba**bgba**g** **b**abgb**ag** ba**b**gb**ag** babg**bag**
提示：
1 <= s.length, t.length <= 1000s和t由英文字母组成
这道题，在我们定义好 dp 数组的含义之后，我们开始思考子序列，子序列最暴力的方式就是一个二叉树，这个二叉树对于每个字符走要和不要两条分路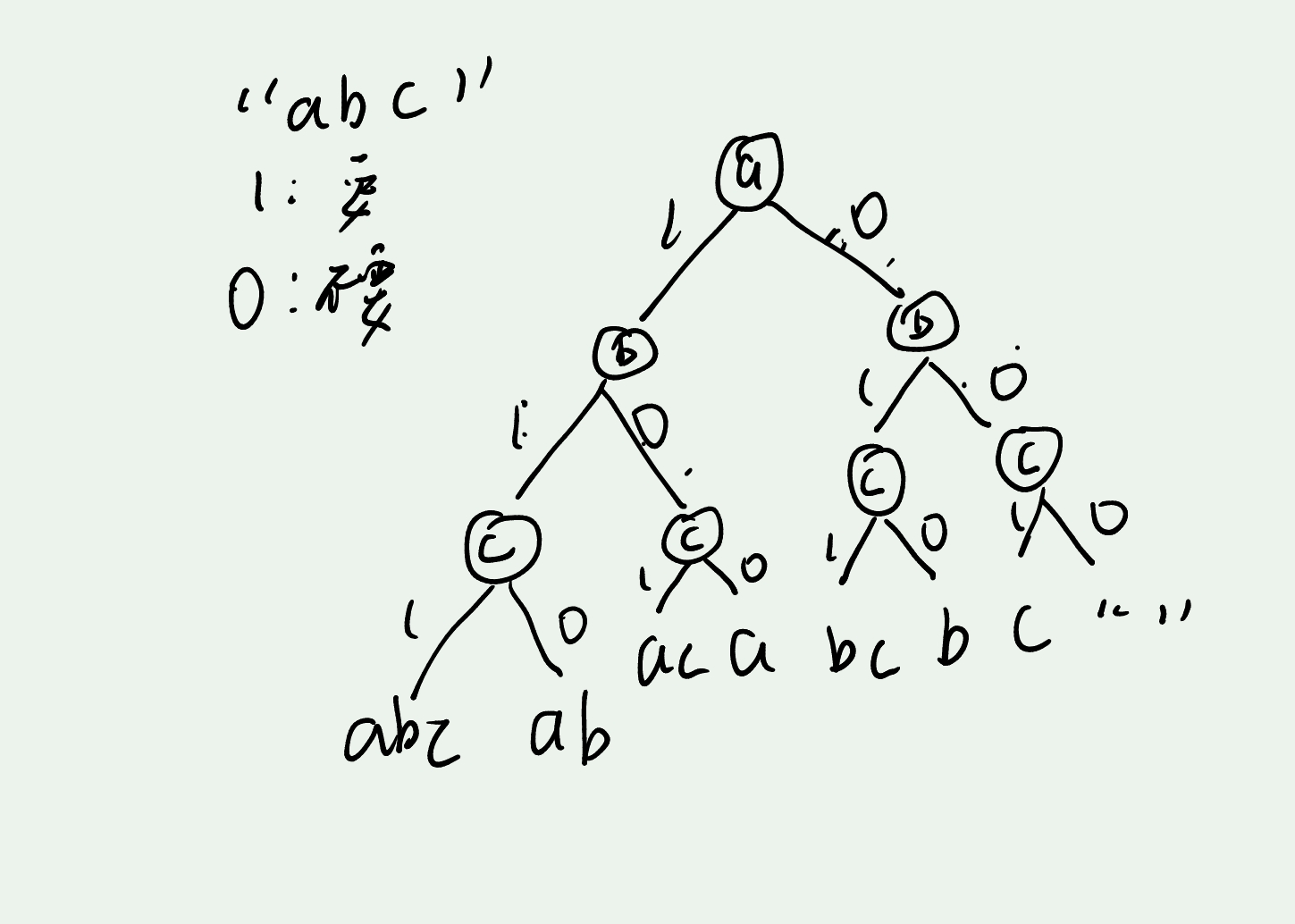 
那么按照我们对于 dp[ i ] [ j ] 的定义，会出现限免两种情况
若 s[0, i-1]== t[0, j-1]
可以要 s[i-1]这最后一个字符，则有 dp[ i ] [ j ] +=dp [ i-1 ] [ j-1]
也可以不要 s[i-1]这最后一个字符，则有 dp[ i ] [ j ] +=dp [ i-1 ] [ j]
s[0, i-1]!= t[0, j-1]
则只能不要 s[i-1]这最后一个字符 dp[ i ] [ j ] +=dp [ i-1 ] [ j]
所以最后 dp[ i ] [ j ] 这个格子与它的左上和上边的格子的值有关联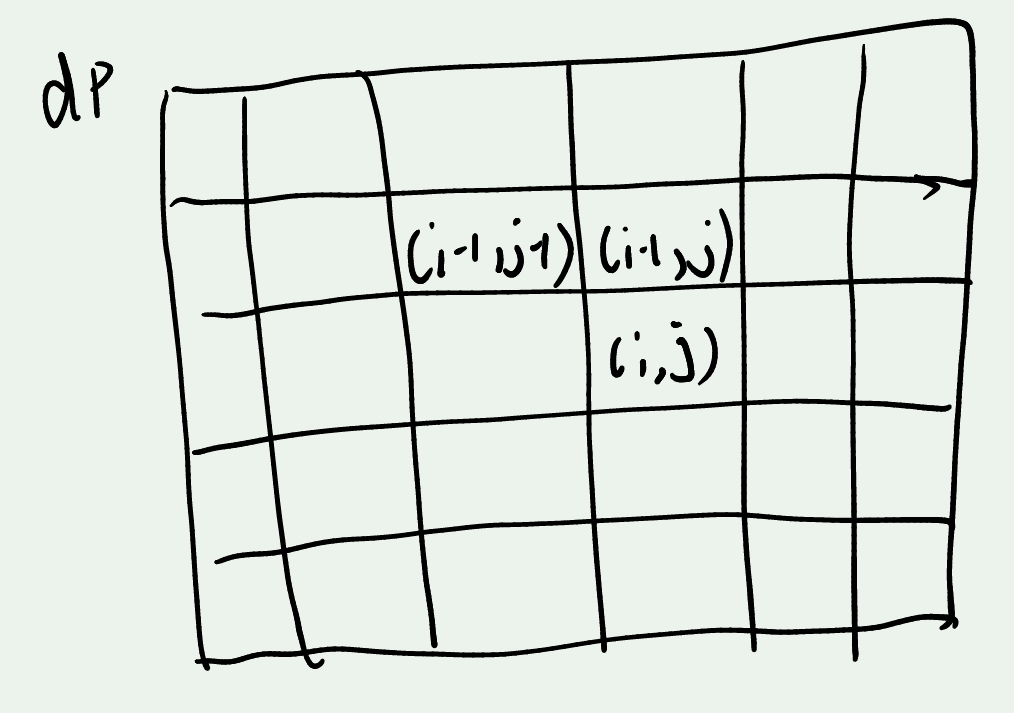 
代码
package main.java.class068;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code01_DistinctSubsequences
* @description: 不同的子序列
* // 给你两个字符串s和t ，统计并返回在s的子序列中t出现的个数
* // 答案对 1000000007 取模
* // 测试链接 : https://leetcode.cn/problems/distinct-subsequences/
* @author: zs宝
* @create: 2025-08-12 09:02
* @Version 1.0
**/
public class Code01_DistinctSubsequences {
class Solution {
public int numDistinct(String s, String t) {
return numDistinct2(s, t);
}
/**
严格按照位置的动态规划
*/
public int numDistinct1(String str, String ttr) {
char[] s = str.toCharArray();
char[] t = ttr.toCharArray();
int m = s.length;
int n = t.length;
//重点：定义dp的含义
//dp[i][j]:s[前缀长度为i]的所有子序列中，有多少个子序列等于t[前缀长度为j]
//即 s[0,i-1]的子序列中出现t[0,j-1]的个数
int[][] dp = new int[m + 1][n + 1];
//dp含义已经定义清楚，那么dp数组的第一行，第一列的值要先求出来
//根据dp含义可知，dp数组的第一列全部为1，第一行除了(0,0)点为1其余全部为0
for (int i = 0; i <= m; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j];
if (s[i - 1] == t[j - 1]) {
dp[i][j]+=dp[i-1][j-1];
}
}
}
return dp[m][n];
}
/**
严格按照位置的动态规划+空间压缩
*/
public int numDistinct2(String str, String ttr) {
char[] s = str.toCharArray();
char[] t = ttr.toCharArray();
int m = s.length;
int n = t.length;
//重点：定义dp的含义
//dp[i][j]:s只包含前缀长度为i的字符的子序列中出现t(只包含前缀长度为j的字符)的个数
//即 s[0,i-1]的子序列中出现t[0,j-1]的个数
//现在将空间进行压缩，二维变成一维。每次循环时含义不变
int[]dp = new int[n + 1];
dp[0]=1;
for (int i = 1; i <= m; i++) {
for (int j = n; j >=1; j--) {
if (s[i - 1] == t[j - 1]) {
dp[j]+=dp[j-1];
}
}
}
return dp[n];
}
}
}2、编辑距离
题目描述： 给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符
示例 1：
输入：word1 = "horse", word2 = "ros" 输出：3 解释： horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
示例 2：
输入：word1 = "intention", word2 = "execution" 输出：5 解释： intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
提示：
0 <= word1.length, word2.length <= 500word1和word2由小写英文字母组成
分析过程 
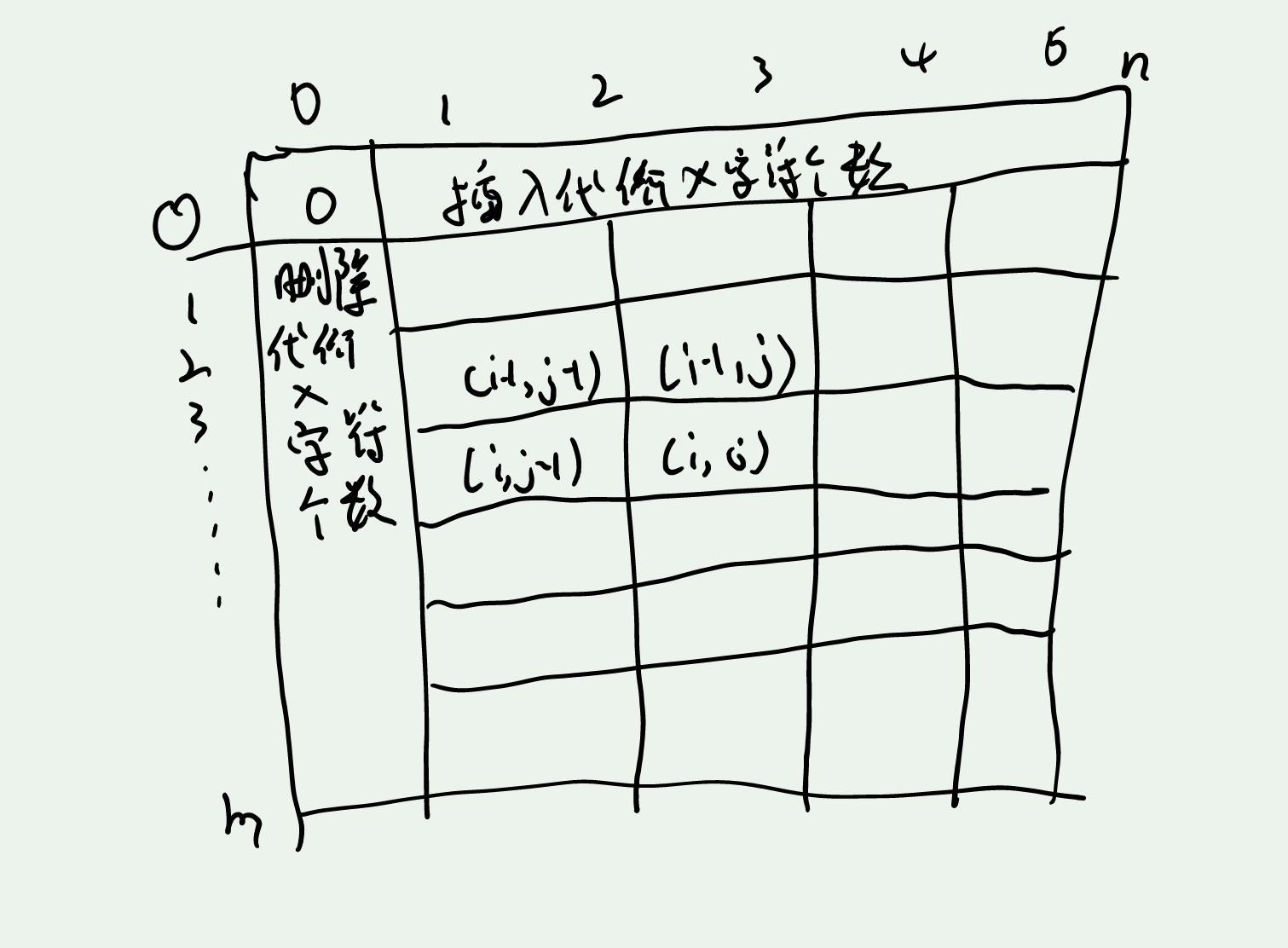
代码
package main.java.class068;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code02_EditDistance
* @description: 编辑距离
* // 给你两个单词 word1 和 word2
* // 请返回将 word1 转换成 word2 所使用的最少代价
* // 你可以对一个单词进行如下三种操作：
* // 插入一个字符，代价a
* // 删除一个字符，代价b
* // 替换一个字符，代价c
* // 测试链接 : https://leetcode.cn/problems/edit-distance/
* @author: zs宝
* @create: 2025-08-12 09:55
* @Version 1.0
**/public class Code02_EditDistance {
class Solution {
public int minDistance(String word1, String word2) {
return editDistance2(word1, word2, 1, 1, 1);
}
//严格按照位置的动态规划
// a : str1中插入1个字符的代价
// b : str1中删除1个字符的代价
// c : str1中改变1个字符的代价
// 返回从str1转化成str2的最低代价
public static int editDistance1(String str1, String str2, int a, int b, int c) {
char[] s1=str1.toCharArray();
char[] s2=str2.toCharArray();
int m=s1.length;
int n=s2.length;
int[][]dp=new int[m+1][n+1];
for(int j=1;j<=n;j++){
dp[0][j]=a*j;
}
for(int i=1;i<=m;i++){
dp[i][0]=b*i;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(s1[i-1]==s2[j-1]){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=Math.min(dp[i-1][j-1]+c,Math.min(dp[i][j-1]+a,dp[i-1][j]+b));
}
}
}
return dp[m][n];
}
//严格按照位置的动态规划+空间压缩
// a : str1中插入1个字符的代价
// b : str1中删除1个字符的代价
// c : str1中改变1个字符的代价
// 返回从str1转化成str2的最低代价
public static int editDistance2(String str1, String str2, int a, int b, int c) {
char[] s1=str1.toCharArray();
char[] s2=str2.toCharArray();
int m=s1.length;
int n=s2.length;
int[]dp=new int[n+1];
//第一行的初始化
for(int j=1;j<=n;j++){
dp[j]=a*j;
}
int leftup=0,backup;
for(int i=1;i<=m;i++){
leftup=dp[0];
dp[0]=b*i;
for(int j=1;j<=n;j++){
backup=dp[j];
if(s1[i-1]==s2[j-1]){
dp[j]=leftup;
}else{
dp[j]=Math.min(leftup+c,Math.min(dp[j-1]+a,dp[j]+b));
}
leftup=backup;
}
}
return dp[n];
}
}
}3、交错字符串
题目描述： 给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：
s = s1 + s2 + ... + snt = t1 + t2 + ... + tm|n - m| <= 1交错 是
s1 + t1 + s2 + t2 + s3 + t3 + ...或者t1 + s1 + t2 + s2 + t3 + s3 + ...
注意：a + b 意味着字符串 a 和 b 连接。
示例 1：
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" 输出：true
示例 2：
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" 输出：false
示例 3：
输入：s1 = "", s2 = "", s3 = "" 输出：true
提示：
0 <= s1.length, s2.length <= 1000 <= s3.length <= 200s1、s2、和s3都由小写英文字母组成
进阶：您能否仅使用 O(s2.length) 额外的内存空间来解决它?
代码
package main.java.class068;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code03_InterleavingString
* @description: 交错字符串
* // 给定三个字符串 s1、s2、s3
* // 请帮忙验证s3是否由s1和s2交错组成
* // 测试链接 : https://leetcode.cn/problems/interleaving-string/
* @author: zs宝
* @create: 2025-08-12 11:03
* @Version 1.0
**/public class Code03_InterleavingString {
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
return isInterleave2(s1,s2,s3);
}
//严格按照位置的动态规划
public boolean isInterleave1(String str1, String str2, String str3) {
if(str1.length()+str2.length()!=str3.length()){
return false;
}
char[]s1=str1.toCharArray();
char[]s2=str2.toCharArray();
char[]s3=str3.toCharArray();
int m=s1.length;
int n=s2.length;
//这个定义很有意思，dp[i][j]为s1[0,i-1]和s2[0,j-1]是否可以交错组成s3[0,i+j-1]
boolean[][]dp=new boolean[m+1][n+1];
dp[0][0]=true;
//分别第一行第一列初始化
for(int i=1;i<=m;i++){
if(s1[i-1]!=s3[i-1]){
break;
}
dp[i][0]=true;
}
for(int j=1;j<=n;j++){
if(s2[j-1]!=s3[j-1]){
break;
}
dp[0][j]=true;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
dp[i][j]=(s1[i-1]==s3[i+j-1] && dp[i-1][j]) || (s2[j-1]==s3[i+j-1] && dp[i][j-1]);
}
}
return dp[m][n];
}
//严格按照位置的动态规划+空间压缩
public boolean isInterleave2(String str1, String str2, String str3) {
if(str1.length()+str2.length()!=str3.length()){
return false;
}
char[]s1=str1.toCharArray();
char[]s2=str2.toCharArray();
char[]s3=str3.toCharArray();
int m=s1.length;
int n=s2.length;
//这个定义很有意思，dp[i][j]为s1[0,i-1]和s2[0,j-1]是否可以交错组成s3[0,i+j-1]
boolean[]dp=new boolean[n+1];
dp[0]=true;
//第一行的初始化
for(int j=1;j<=n;j++){
if(s2[j-1]!=s3[j-1]){
break;
}
dp[j]=true;
}
for(int i=1;i<=m;i++){
dp[0]=s1[i-1]==s3[i-1]&& dp[0];
for(int j=1;j<=n;j++){
dp[j]=(s1[i-1]==s3[i+j-1] && dp[j]) || (s2[j-1]==s3[i+j-1] && dp[j-1]);
}
}
return dp[n];
}
}
}4、有效涂色问题
这是一个大厂面试的题（无测试链接）
给定 n、m 两个参数 一共有 n 个格子，每个格子可以涂上一种颜色，颜色在 m 种里选 当涂满 n 个格子，并且 m 种颜色都使用了，叫一种有效方法 求一共有多少种有效的涂色方法 1 <= n, m <= 5000 结果比较大请 % 1000000007 之后返回 对数器验证
注意 dp 的定义，这道题最开始写的时候对于 dp 的定义都写错了。
package main.java.class068;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code04_FillCellsUseAllColorsWays
* @description: 有效涂色问题
* // 给定n、m两个参数
* // 一共有n个格子，每个格子可以涂上一种颜色，颜色在m种里选
* // 当涂满n个格子，并且m种颜色都使用了，叫一种有效方法
* // 求一共有多少种有效的涂色方法
* // 1 <= n, m <= 5000
* // 结果比较大请 % 1000000007 之后返回
* // 对数器验证
* @author: zs宝
* @create: 2025-08-12 20:23
* @Version 1.0
**/public class Code04_FillCellsUseAllColorsWays {
public static int MOD=1000000007;
public static int MAXN=5001;
public static int [][]dp=new int[MAXN][MAXN];
/**
* 动态规划解法
* @param n
* @param m
* @return
*/
public static int ways2(int n, int m) {
//定义dp[i][j]:在前i个格子，涂满了j中颜色的有效涂色数量
//首先定义第一行第一列，但是我们发现当i=0,或者j=0时，这对题本身而言根本就没有意义，它就是0
//要想题目本身有意义，起码的为1
//因此分析当i=1时，除了j=1时有意义，其余时候根本无意义，全部为0
//当j=1时，这个有意义
for(int i=1;i<=n;i++){
dp[i][1]=m;
}
for(int i=2;i<=n;i++){
for(int j=2;j<=m;j++){
//情况1：当前i-1个格子以及涂满了j中颜色时，那么第i个格子只需要j中颜色随便选一个涂就可以
dp[i][j]=(int)(((long)dp[i-1][j]*j)%MOD);
//情况2：当前i-1个格子只涂了j-1种颜色，那么第i个格子还需要再涂一种其余颜色即可
dp[i][j]=(int)((((long)dp[i-1][j-1]*(m-j+1))+dp[i][j])%MOD);
}
}
return dp[n][m];
}
// 暴力方法：找到s1的所有子串
// 为了验证
public static int ways1(int n, int m) {
return f(new int[n], new boolean[m + 1], 0, n, m);
}
// 把所有填色的方法暴力枚举
// 然后一个一个验证是否有效
// 这是一个带路径的递归
// 无法改成动态规划
public static int f(int[] path, boolean[] set, int i, int n, int m) {
if (i == n) {
Arrays.fill(set, false);
int colors = 0;
for (int c : path) {
if (!set[c]) {
set[c] = true;
colors++;
}
}
return colors == m ? 1 : 0;
} else {
int ans = 0;
for (int j = 1; j <= m; j++) {
path[i] = j;
ans += f(path, set, i + 1, n, m);
}
return ans;
}
}
public static void main(String[] args) {
// 测试的数据量比较小
// 那是因为数据量大了，暴力方法过不了
// 但是这个数据量足够说明正式方法是正确的
int N = 9;
int M = 9;
System.out.println("功能测试开始");
for (int n = 1; n <= N; n++) {
for (int m = 1; m <= M; m++) {
int ans1 = ways1(n, m);
int ans2 = ways2(n, m);
if (ans1 != ans2) {
System.out.println("出错了!");
}
}
}
System.out.println("功能测试结束");
System.out.println("性能测试开始");
int n = 5000;
int m = 4877;
System.out.println("n : " + n);
System.out.println("m : " + m);
long start = System.currentTimeMillis();
int ans = ways2(n, m);
long end = System.currentTimeMillis();
System.out.println("取模之后的结果 : " + ans);
System.out.println("运行时间 : " + (end - start) + " 毫秒");
System.out.println("性能测试结束");
}
}5、删除至少几个字符可以变成另一个字符串的子串
这是一个大厂面试的题（无测试链接）
给定两个字符串 s 1 和 s 2 返回 s 1 至少删除多少字符可以成为 s 2 的子串 对数器验证
注意 dp 的定义，这种定义很少见
package main.java.class068;
import java.util.ArrayList;
import java.util.List;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code05_MinimumDeleteBecomeSubstring
* @description: 删除至少几个字符可以变成另一个字符串的子串
* // 给定两个字符串s1和s2
* // 返回s1至少删除多少字符可以成为s2的子串
* // 对数器验证
* @author: zs宝
* @create: 2025-08-12 20:57
* @Version 1.0
**/public class Code05_MinimumDeleteBecomeSubstring {
/**
* 动态规划
* @param str1
* @param str2
* @return
*/
public static int minDelete2(String str1, String str2) {
char[] s1=str1.toCharArray();
char[] s2=str2.toCharArray();
int n=s1.length;
int m=s2.length;
//定义dp[i][j]:s1[0,i-1]至少要删掉几个字符才可以为s2[0,j-1]的后缀串
//即s1[前缀长度为i]至少删除多少字符，可以变成s2[前缀长度为j]的任意后缀串
int[][]dp=new int[n+1][m+1];
//第一行第一列的初始化
/*for(int j=0;j<=m;j++){
dp[0][j]=0; }*/ /*for(int i=0;i<=n;i++){ dp[i][0]=i; }*/ for(int i=1;i<=n;i++){
dp[i][0]=i;
for(int j=1;j<=m;j++){
if(s1[i-1]==s2[j-1]){
dp[i][j]=dp[i-1][j-1];
}else {
dp[i][j]=1+dp[i-1][j];
}
}
}
int ans=Integer.MAX_VALUE;
for(int j=0;j<=m;j++){
ans=Math.min(ans,dp[n][j]);
}
return ans;
}
// 暴力方法
// 为了验证
public static int minDelete1(String s1, String s2) {
List<String> list = new ArrayList<>();
f(s1.toCharArray(), 0, "", list);
// 排序 : 长度大的子序列先考虑
// 因为如果长度大的子序列是s2的子串
// 那么需要删掉的字符数量 = s1的长度 - s1子序列长度
// 子序列长度越大，需要删掉的字符数量就越少
// 所以长度大的子序列先考虑
list.sort((a, b) -> b.length() - a.length());
for (String str : list) {
if (s2.indexOf(str) != -1) {
// 检查s2中，是否包含当前的s1子序列str
return s1.length() - str.length();
}
}
return s1.length();
}
// 生成s1字符串的所有子序列串
public static void f(char[] s1, int i, String path, List<String> list) {
if (i == s1.length) {
list.add(path);
} else {
f(s1, i + 1, path, list);
f(s1, i + 1, path + s1[i], list);
}
}
// 为了验证
// 生成长度为n，有v种字符的随机字符串
public static String randomString(int n, int v) {
char[] ans = new char[n];
for (int i = 0; i < n; i++) {
ans[i] = (char) ('a' + (int) (Math.random() * v));
}
return String.valueOf(ans);
}
// 为了验证
// 对数器
public static void main(String[] args) {
// 测试的数据量比较小
// 那是因为数据量大了，暴力方法过不了
// 但是这个数据量足够说明正式方法是正确的
int n = 12;
int v = 3;
int testTime = 20000;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int len1 = (int) (Math.random() * n) + 1;
int len2 = (int) (Math.random() * n) + 1;
String s1 = randomString(len1, v);
String s2 = randomString(len2, v);
int ans1 = minDelete1(s1, s2);
int ans2 = minDelete2(s1, s2);
if (ans1 != ans2) {
System.out.println("出错了!");
}
}
System.out.println("测试结束");
}
}