核心思想

尝试函数有 1 个可变参数可以完全决定返回值，进而可以改出 1 维动态规划表的实现同理尝试函数有 2 个可变参数可以完全决定返回值，那么就可以改出 2 维动态规划的实现同理尝试函数有 3 个可变参数可以完全决定返回值，那么就可以改出 3 维动态规划的实现

大体过程都是：写出尝试递归记忆化搜索 (从顶到底的动态规划) 严格位置依赖的动态规划 (从底到顶的动态规划) 空间、时间的更多优化

原理完全一样，直接看题目吧！

例题

1、一和零

题目描述：给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中最多有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集。

示例 1：

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3 输出：4 解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = ["10", "0", "1"], m = 1, n = 1 输出：2 解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

提示：

1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 '0' 和 '1' 组成
1 <= m, n <= 100

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 474 + 一和零
🧠 题目关键词（原文关键词）	二进制字符串数组 `strs`，子集中最多有 `m` 个 `0` 和 `n` 个 `1` ，最大子集
🧩 抽象问题类型（题目本质）	0/1 背包问题
🔍 数据规模 / 限制	- `1 <= strs.length <= 600` - `1 <= strs[i].length <= 100` - `strs[i]` 仅由 `'0'` 和 `'1'` 组成 - `1 <= m, n <= 100`
🧭 我的初步思路	要或者不要的二叉树
✅ 正确解法类型	动态规划
❗ 没想到的原因	暴力递归这块设置的参数太多太复杂，可以简化
📦 归入的题型分类	动态规划
🧠 触发词（以后遇到就联想）	“选择若干项 + 多维资源上限（m 个 0、n 个 1）+ 最大数量” → 多维 0/1 背包
🧪 解法一句话总结	每个字符串，选择要或者不要的时候，分类讨论这样您呢个拿到的最大字符串，注意每次要的时候，当前字符串中的 0 或者 1 的数量不能超过剩余还可以容纳的量

这里对于最开始的递归，我写的是 f 1（strs, m, n, i, z, o）表示字符串数组 strs ，题目给的总要求是 0/1数量不能超过 m, n ，当前在 strs 数组的 i 位置，已经使用了 z 个 0，o 个 1。这种表述方式与下面的 f 1 (strs, i, z, o) 表示在 i 位置的还剩下 z, o 个 0/1 可以供使用，两者表达的意思其实几乎一样，但是明显后者更贱简洁凝练一点。啊啊啊啊

 package main.java.class069;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code01_OnesAndZeroes  
  * @description: 一和零(多维费用背包)  
  * // 给你一个二进制字符串数组 strs 和两个整数 m 和 n  
  * // 请你找出并返回 strs 的最大子集的长度  
  * // 该子集中 最多 有 m 个 0 和 n 个 1  
  * // 如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集  
  * // 测试链接 : https://leetcode.cn/problems/ones-and-zeroes/  
  * @author: zs宝  
  * @create: 2025-08-15 10:23  
  * @Version 1.0  
  **/public class Code01_OnesAndZeroes {  
     class Solution {  
         public static int findMaxForm(String[] strs, int m, int n) {  
             return findMaxForm4(strs,m,n);  
         }  
   
         public static int zeros,ones;  
         //求解每个字符串中有多少0/1  
         public static void zerosAndOnes(String str) {  
             zeros=0;  
             ones=0;  
             for(int i=0;i<str.length();i++){  
                 if(str.charAt(i)=='0'){  
                     zeros++;  
                 }else{  
                     ones++;  
                 }  
             }  
         }  
   
         /**  
          暴力递归的方式  
          */  
         public static int findMaxForm1(String[] strs, int m, int n) {  
             return f1(strs,0,m,n);  
         }  
         /**  
          i：第i个字符串  
          z: 还剩多少个0可以使用  
          o：还剩多少个1可以使用  
          定义为strs[i........]自由选择，0和1的数量不超过z,o。最多可以选择多少个字符串  
          */  
         public static int f1(String[] strs,int i, int z, int o){  
             if(i==strs.length ){  
                 return 0;  
             }  
             //接下来判定当前字符串是要还是不要  
             int ans=0;  
             //如果不要  
             ans=f1(strs,i+1,z,o);  
             //如果要  
   
             zerosAndOnes(strs[i]);  
             if(zeros<=z && ones<= o){  
                 ans=Math.max(ans,1+f1(strs,i+1,z-zeros,o-ones));  
             }  
             return ans;  
         }  
   
         /**  
          记忆化搜索：由暴力递归优化而来  
          */  
         public static int findMaxForm2(String[] strs, int m, int n) {  
             int len=strs.length;  
             int[][][]dp=new int[len+1][m+1][n+1];  
             for(int i=0;i<=len;i++){  
                 for(int z=0;z<=m;z++){  
                     for(int o=0;o<=n;o++){  
                         dp[i][z][o]=-1;  
                     }  
                 }  
             }  
             return f2(strs,0,m,n,dp);  
         }  
         /**  
          i：第i个字符串  
          z: 还剩多少个0可以使用  
          o：还剩多少个1可以使用  
          定义为strs[i........]自由选择，0和1的数量不超过z,o。最多可以选择多少个字符串  
          */  
         public static int f2(String[] strs,int i, int z, int o,int[][][]dp){  
             if(i==strs.length ){  
                 return 0;  
             }  
             if(dp[i][z][o]!=-1){  
                 return dp[i][z][o];  
             }  
             //接下来判定当前字符串是要还是不要  
             int ans=0;  
             //如果不要  
             ans=f2(strs,i+1,z,o,dp);  
             //如果要  
             zerosAndOnes(strs[i]);  
             if(zeros<=z && ones<= o){  
                 ans=Math.max(ans,1+f2(strs,i+1,z-zeros,o-ones,dp));  
             }  
             dp[i][z][o]=ans;  
             return ans;  
         }  
   
   
         /**  
          严格依赖位置的动态规划：由记忆化搜索优化而来  
          */  
         public static int findMaxForm3(String[] strs, int m, int n) {  
             int len=strs.length;  
             int[][][]dp=new int[len+1][m+1][n+1];  
             for(int i=len-1;i>=0;i--){  
                 for(int z=0;z<=m;z++){  
                     for(int o=0;o<=n;o++){  
                         zerosAndOnes(strs[i]);  
                         dp[i][z][o]=dp[i+1][z][o];  
                         if(zeros<=z && ones<=o){  
                             dp[i][z][o]=Math.max(dp[i][z][o],1+dp[i+1][z-zeros][o-ones]);  
                         }  
                     }  
                 }  
             }  
             return dp[0][m][n];  
         }  
   
         /**  
          严格依赖位置的动态规划+空间压缩  
          */  
         public static int findMaxForm4(String[] strs, int m, int n) {  
             int len=strs.length;  
             int[][]dp=new int[m+1][n+1];  
             for(int i=len-1;i>=0;i--){  
                 for(int z=m;z>=0;z--){  
                     for(int o=n;o>=0;o--){  
                         zerosAndOnes(strs[i]);  
                         dp[z][o]=dp[z][o];  
                         if(zeros<=z && ones<=o){  
                             dp[z][o]=Math.max(dp[z][o],1+dp[z-zeros][o-ones]);  
                         }  
                     }  
                 }  
             }  
             return dp[m][n];  
         }  
     }  
 }

2、盈利计划

题目描述：集团里有 n 名员工，他们可以完成各种各样的工作创造利润。

第 i 种工作会产生 profit[i] 的利润，它要求 group[i] 名成员共同参与。如果成员参与了其中一项工作，就不能参与另一项工作。

工作的任何至少产生 minProfit 利润的子集称为 盈利计划 。并且工作的成员总数最多为 n 。

有多少种计划可以选择？因为答案很大，所以 返回结果模 10^9 + 7 的值。

示例 1：

输入：n = 5, minProfit = 3, group = [2,2], profit = [2,3] 输出：2 解释：至少产生 3 的利润，该集团可以完成工作 0 和工作 1 ，或仅完成工作 1 。总的来说，有两种计划。

示例 2：

输入：n = 10, minProfit = 5, group = [2,3,5], profit = [6,7,8] 输出：7 解释：至少产生 5 的利润，只要完成其中一种工作就行，所以该集团可以完成任何工作。有 7 种可能的计划：(0)，(1)，(2)，(0,1)，(0,2)，(1,2)，以及 (0,1,2) 。

提示：

1 <= n <= 100
0 <= minProfit <= 100
1 <= group.length <= 100
1 <= group[i] <= 100
profit.length == group.length
0 <= profit[i] <= 100

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 879 + 盈利计划
🧠 题目关键词（原文关键词）	至少 minProfit、成员上限 n、选择子集、方案数、取模 1e9+7
🧩 抽象问题类型（题目本质）	二维约束 + 计数型 0/1 背包（方案数 DP）：容量1=人数、容量2=利润（向上截断到 minProfit）
🔍 数据规模 / 限制	- `1 <= n <= 100` - `0 <= minProfit <= 100` - `1 <= group.length <= 100` - `1 <= group[i] <= 100` - `profit.length == group.length` - `0 <= profit[i] <= 100`
🧭 我的初步思路	暴力递归
✅ 正确解法类型	动态规划
❗ 没想到的原因	暴力递归的出递归条件没想全，想错误
📦 归入的题型分类	动态规划类
🧠 触发词（以后遇到就联想）	“人数上限 + 利润下限 + 方案数” → 多维容量的计数背包；利润维度截断到 minProfit
🧪 解法一句话总结	定义三维动态规划数组 `dp[i][j][k]` 表示考虑前 `i` 个任务、使用 `j` 个成员、获得至少 `k` 的利润的方案数，状态转移时枚举第 `i` 个任务选或不选，最终累加所有 `dp[m][j][minProfit]` 得到答案。

这道题在最开始写暴力递归哪里，在找出递归的边界条件处一直少考虑了数组的边界位置不能越过，但是当时报错却一直没有想到，这实在是不应该的事情，因为已经写过多道递归，且每道递归涉及到数组都一定会考虑边界的问题。啊啊啊啊，好烦啊。

递归考虑出递归的条件顺序

有数组方面的，优先考虑越界位置的问题
考虑题目本身达到要求的含义返回值

代码

 package main.java.class069;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code02_ProfitableSchemes  
  * @description: 盈利计划(多维费用背包)  
  * // 集团里有 n 名员工，他们可以完成各种各样的工作创造利润  
  * // 第 i 种工作会产生 profit[i] 的利润，它要求 group[i] 名成员共同参与  
  * // 如果成员参与了其中一项工作，就不能参与另一项工作  
  * // 工作的任何至少产生 minProfit 利润的子集称为 盈利计划  
  * // 并且工作的成员总数最多为 n  
  * // 有多少种计划可以选择？因为答案很大，答案对 1000000007 取模  
  * // 测试链接 : https://leetcode.cn/problems/profitable-schemes/  
  * @author: zs宝  
  * @create: 2025-08-16 09:30  
  * @Version 1.0  
  **/public class Code02_ProfitableSchemes {  
     class Solution {  
         public static int profitableSchemes(int n, int minProfit, int[] group, int[] profit) {  
             return profitableSchemes4(n, minProfit, group, profit);  
         }  
   
         /**  
          暴力递归解法：超时  
          */  
         public static int profitableSchemes1(int n, int minProfit, int[] group, int[] profit) {  
             return f1(n, minProfit, group, profit, 0);  
         }  
   
         /**  
          n：还剩n个人  
          minProfit:还差多少利润  
          i：当前第几个任务  
          */  
         public static int f1(int n, int minProfit, int[] group, int[] profit, int i) {  
             if (n <= 0) {  
                 return minProfit <= 0 ? 1 : 0;  
             }  
             if (i == group.length) {  
                 return minProfit <= 0 ? 1 : 0;  
             }  
             //执行当前任务，或者不执行当前任务  
             int ans = 0;  
             ans += f1(n, minProfit, group, profit, i + 1);  
             if (group[i] <= n) {  
                 ans += f1(n - group[i], minProfit - profit[i], group, profit, i + 1);  
             }  
             return ans;  
         }  
   
         /**  
          记忆化搜索：由暴力递归优化而来  
          */  
   
         public static int MOD = 1000000007;  
   
         public static int profitableSchemes2(int n, int minProfit, int[] group, int[] profit) {  
             int m = group.length;  
             int[][][] dp = new int[m + 1][n + 1][minProfit + 1];  
             for (int i = 0; i <= m; i++) {  
                 for (int j = 0; j <= n; j++) {  
                     for (int k = 0; k <= minProfit; k++) {  
                         dp[i][j][k] = -1;  
                     }  
                 }  
             }  
             return f2(group, profit, 0, n, minProfit, dp);  
         }  
   
         /**  
          i：当前第几个任务  
          j：还剩j个人  
          k:还差多少利润  
          */  
         public static int f2(int[] group, int[] profit, int i, int j, int k, int[][][] dp) {  
             if (j <= 0) {  
                 return k == 0 ? 1 : 0;  
             }  
             if (i == group.length) {  
                 return k == 0 ? 1 : 0;  
             }  
             if (dp[i][j][k] != -1) {  
                 return dp[i][j][k];  
             }  
             //执行当前任务，或者不执行当前任务  
             int ans = 0;  
             ans = (ans + f2(group, profit, i + 1, j, k, dp)) % MOD;  
             if (group[i] <= j) {  
                 //不能让k<0,超出数组边界  
                 ans = (ans + f2(group, profit, i + 1, j - group[i], Math.max(0, k - profit[i]), dp)) % MOD;  
             }  
             dp[i][j][k] = ans;  
             return ans;  
         }  
   
         /**  
          严格按照位置的动态规划：由记忆化搜索优化而来  
          */  
         public static int profitableSchemes3(int n, int minProfit, int[] group, int[] profit) {  
             int m = group.length;  
             int[][][] dp = new int[m + 1][n + 1][minProfit + 1];  
             for (int j = 0; j <= n; j++) {  
                 dp[m][j][0] = 1;  
             }  
             for (int i = m - 1; i >= 0; i--) {  
                 for (int j = 0; j <=n; j++) {  
                     for (int k = 0; k <=minProfit; k++) {  
                         dp[i][j][k] = dp[i + 1][j][k];  
                         if (group[i] <= j) {  
                             dp[i][j][k] = (dp[i][j][k] + dp[i + 1][j - group[i]][Math.max(0, k - profit[i])]) % MOD;  
                         }  
                     }  
                 }  
             }  
             return dp[0][n][minProfit];  
         }  
   
         /**  
          严格按照位置的动态规划+空间压缩  
          */  
         public static int profitableSchemes4(int n, int minProfit, int[] group, int[] profit) {  
             int m = group.length;  
             int[][] dp = new int[n + 1][minProfit + 1];  
             for (int j = 0; j <= n; j++) {  
                 dp[j][0] = 1;  
             }  
             for (int i = m - 1; i >= 0; i--) {  
                 for (int j = n; j >=0; j--) {  
                     for (int k =minProfit; k >=0; k--) {  
                         if (group[i] <= j) {  
                             dp[j][k] = (dp[j][k] + dp[j - group[i]][Math.max(0, k - profit[i])]) % MOD;  
                         }  
                     }  
                 }  
             }  
             return dp[n][minProfit];  
         }  
     }  
 }

3、骑士在棋盘上的概率

题目描述：在一个 n x n 的国际象棋棋盘上，一个骑士从单元格 (row, column) 开始，并尝试进行 k 次移动。行和列是 从 0 开始 的，所以左上单元格是 (0,0) ，右下单元格是 (n - 1, n - 1) 。

象棋骑士有8种可能的走法，如下图所示。每次移动在基本方向上是两个单元格，然后在正交方向上是一个单元格。

每次骑士要移动时，它都会随机从8种可能的移动中选择一种(即使棋子会离开棋盘)，然后移动到那里。

骑士继续移动，直到它走了 k 步或离开了棋盘。

返回 骑士在棋盘停止移动后仍留在棋盘上的概率 。

示例 1：

输入: n = 3, k = 2, row = 0, column = 0 输出: 0.0625 解释: 有两步(到(1,2)，(2,1))可以让骑士留在棋盘上。在每一个位置上，也有两种移动可以让骑士留在棋盘上。骑士留在棋盘上的总概率是0.0625。

示例 2：

输入: n = 1, k = 0, row = 0, column = 0 输出: 1.00000

提示:

1 <= n <= 25
0 <= k <= 100
0 <= row, column <= n - 1

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 688 - Knight Probability in Chessboard（骑士在棋盘上的概率）
🧠 题目关键词（原文关键词）	骑士、国际象棋、8 个走法、k 步、留在棋盘上的概率
🧩 抽象问题类型（题目本质）	概率 DP / 马尔可夫链在有限步内的留存概率（状态转移图）
🔍 数据规模 / 限制	1 ≤ n ≤ 25，0 ≤ k ≤ 100
🧭 我的初步思路	暴力递归
✅ 正确解法类型	动态规划
❗ 没想到的原因	识别出来了
📦 归入的题型分类	动态规划
🧠 触发词（以后遇到就联想）	“走 k 步 + 等概率转移 + 留在网格上的概率” → 分层概率 DP
🧪 解法一句话总结	定义递归函数为在 n*n 的格子上，在还剩 k 步的情况下，在（i, j) 位置向八个方向移动后仍留在棋盘上的概率

此题, 如果要写严格按照位置依赖的动态规划, 其位置要与八个位置有关进行判定,复杂且不好统计, 且时间复杂度提升并不大, 因此只写到了记忆化搜索.

 package main.java.class069;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code03_KnightProbabilityInChessboard  
  * @description: 骑士在棋盘上的概率  
  * // n * n的国际象棋棋盘上，一个骑士从单元格(row, col)开始，并尝试进行 k 次移动  
  * // 行和列从0开始，所以左上单元格是 (0,0)，右下单元格是 (n-1, n-1)  
  * // 象棋骑士有8种可能的走法。每次移动在基本方向上是两个单元格，然后在正交方向上是一个单元格  
  * // 每次骑士要移动时，它都会随机从8种可能的移动中选择一种，然后移动到那里  
  * // 骑士继续移动，直到它走了 k 步或离开了棋盘  
  * // 返回 骑士在棋盘停止移动后仍留在棋盘上的概率  
  * // 测试链接 : https://leetcode.cn/problems/knight-probability-in-chessboard/  
  * @author: zs宝  
  * @create: 2025-08-17 09:03  
  * @Version 1.0  
  **/public class Code03_KnightProbabilityInChessboard {  
     class Solution {  
         public double knightProbability(int n, int k, int row, int column) {  
             return knightProbability2(n,k,row,column);  
         }  
   
   
         /**  
          暴力递归：超时  
          */  
         public double knightProbability1(int n, int k, int row, int column) {  
             return f1(n,k,row,column);  
         }  
         //在n*n的格子上，在还剩k步的情况下，在（i,j)位置向八个方向移动后仍留在棋盘上的概率  
         public double f1(int n, int k, int i, int j) {  
             if(i<0 || j<0 || i>=n || j >=n){  
                 return 0;  
             }  
             if(k<=0){  
                 return 1;  
             }  
   
             double p=(f1(n,k-1,i-2,j-1)+f1(n,k-1,i-2,j+1)+f1(n,k-1,i-1,j+2)+f1(n,k-1,i+1,j+2)+  
                     f1(n,k-1,i+2,j+1)+f1(n,k-1,i+2,j-1)+f1(n,k-1,i+1,j-2)+f1(n,k-1,i-1,j-2))*(1.0/8);  
   
             return p;  
         }  
   
   
         /**  
          记忆化搜索：由暴力递归优化而来  
          */  
         public double knightProbability2(int n, int path, int row, int column) {  
             double[][][]dp=new double[path+1][n+1][n+1];  
             for(int k=0;k<=path;k++){  
                 for(int i=0;i<=n;i++){  
                     for(int j=0;j<=n;j++){  
                         dp[k][i][j]=-1;  
                     }  
                 }  
             }  
             return f2(n,path,row,column,dp);  
         }  
         //在n*n的格子上，在还剩k步的情况下，在（i,j)位置向八个方向移动后仍留在棋盘上的概率  
         public double f2(int n, int k, int i, int j,double[][][]dp) {  
             if(i<0 || j<0 || i>=n || j >=n){  
                 return 0;  
             }  
             if(k<=0){  
                 return 1;  
             }  
   
             if(dp[k][i][j]!=-1){  
                 return dp[k][i][j];  
             }  
   
             double p=(f2(n,k-1,i-2,j-1,dp)+f2(n,k-1,i-2,j+1,dp)+f2(n,k-1,i-1,j+2,dp)+f2(n,k-1,i+1,j+2,dp)+  
                     f2(n,k-1,i+2,j+1,dp)+f2(n,k-1,i+2,j-1,dp)+f2(n,k-1,i+1,j-2,dp)+f2(n,k-1,i-1,j-2,dp))*(1.0/8);  
             dp[k][i][j]=p;  
             return p;  
         }  
         }  
 }

4、矩阵中和能被 K 整除的路径

题目描述：给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发，每一步只能往下或者往右，你想要到达终点 (m - 1, n - 1) 。

请你返回路径和能被 k 整除的路径数目，由于答案可能很大，返回答案对 109 + 7 取余的结果。

示例 1：

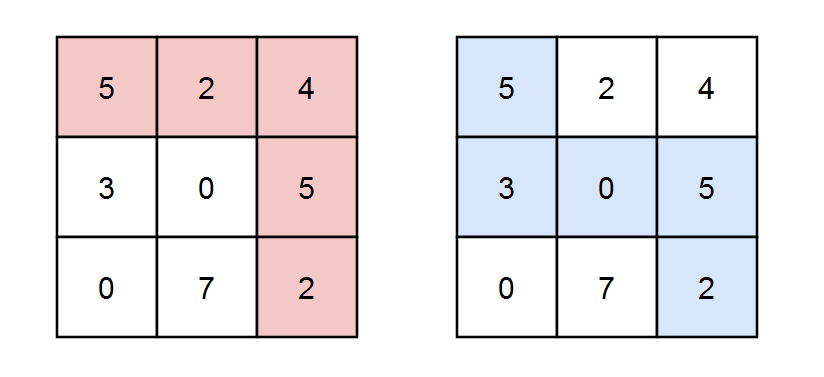
输入：grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3 输出：2 解释：有两条路径满足路径上元素的和能被 k 整除。第一条路径为上图中用红色标注的路径，和为 5 + 2 + 4 + 5 + 2 = 18 ，能被 3 整除。第二条路径为上图中用蓝色标注的路径，和为 5 + 3 + 0 + 5 + 2 = 15 ，能被 3 整除。

示例 2：

输入：grid = [[0,0]], k = 5 输出：1 解释：红色标注的路径和为 0 + 0 = 0 ，能被 5 整除。

示例 3：

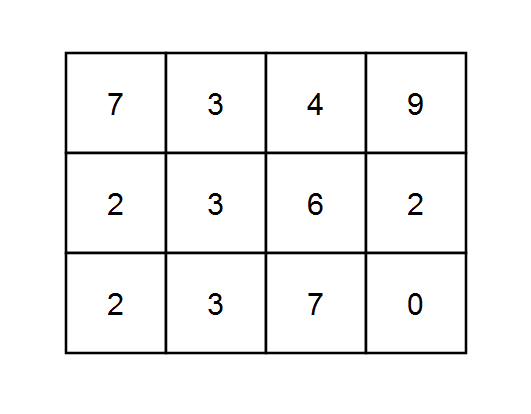
输入：grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1 输出：10 解释：每个数字都能被 1 整除，所以每一条路径的和都能被 k 整除。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 5 * 104
1 <= m * n <= 5 * 104
0 <= grid[i][j] <= 100
1 <= k <= 50

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 2435 + 矩阵中和能被 K 整除的路径
🧠 题目关键词（原文关键词）	路径和能被 `k` 整除的路径数目，从起点 `(0, 0)` 出发，每一步只能往下或者往右，你想要到达终点 `(m - 1, n - 1)` 。
🧩 抽象问题类型（题目本质）	带取模余数维度的路径计数 DP（网格 DP + 余数状态）
🔍 数据规模 / 限制	1 ≤ m·n ≤ 5×10⁴，0 ≤ gridi ≤ 100，1 ≤ k ≤ 50
🧭 我的初步思路	暴力递归
✅ 正确解法类型	动态规划
❗ 没想到的原因	递归定义想法出错
📦 归入的题型分类	动态规划类
🧠 触发词（以后遇到就联想）	“网格只能右/下 + 路径和对 k 的约束（可被整除/余数）” → DP 加余数维
🧪 解法一句话总结	用 `dp[i][j][r]` 表示从 (i,j) 出发到终点，路径和 mod k = r 的路径数

这道题最开始的暴力递归都想错了，想成了在 (i, j) 位置到达终点的路径累加和可以整除 k 的条数，这样的定义与题目求的东西没有差别，但是在网格中移动过程中，也就是在递归到其它格子中，就有一个问题，不同格子上的值不同，你从 (i, j ) 位置到达目标点的路径和可以被 k 整除不等于从起点位置的到达目标点的路径和仍然可以被 k 整除，我们这个 k 从来没有变过。即上述定义在移动过程中，并没有带上已经走过的格子的路径状态，于是直接看整除不行，那么就转换思路，要带上每个格子的状态表示，又是累加和，就用余数来进行表示，当前走过的路径和整除 k 余数多少，那么为了能让到达终点的的累加和可以整除 k, 所以剩下的路径和需要除以 k 以达到多少的余数，走过的路径和与未走的还差的路径和之间的余数室友关联的，其计算公式为（其中 r 表示前面走过的路径和希望接下来的路径和可以达到的余数）

 //累和当前点后，接着向目标点出发，后续需要凑出来的余数  
 int need = (k + r - (grid[i][j] % k)) % k;

最终代码如下：

 package main.java.class069;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code04_PathsDivisibleByK  
  * @description: 矩阵中和能被 K 整除的路径  
  * // 给一个下标从0开始的 n * m 整数矩阵 grid 和一个整数 k  
  * // 从起点(0,0)出发，每步只能往下或者往右，你想要到达终点(m-1, n-1)  
  * // 请你返回路径和能被 k 整除的路径数目  
  * // 答案对 1000000007 取模  
  * // 测试链接 : https://leetcode.cn/problems/paths-in-matrix-whose-sum-is-divisible-by-k/  
  * @author: zs宝  
  * @create: 2025-08-17 09:39  
  * @Version 1.0  
  **/public class Code04_PathsDivisibleByK {  
     class Solution {  
         public static int MOD = 1000000007;  
   
         public static int numberOfPaths(int[][] grid, int k) {  
             return numberOfPaths3(grid, k);  
         }  
   
         /**  
          暴力递归：超时  
          */  
         public static int numberOfPaths1(int[][] grid, int k) {  
             int n = grid.length;  
             int m = grid[0].length;  
             return f1(grid, n, m, k, 0, 0, 0);  
         }  
   
         /**  
          从(i,j)位置到目标点（n-1,m-1）有多少条路径，累和整除k的余数是r  
          */        public static int f1(int[][] grid, int n, int m, int k, int i, int j, int r) {  
             if (i == n - 1 && j == m - 1) {  
                 return grid[i][j] % k == r ? 1 : 0;  
             }  
             //累和当前点后，接着向目标点出发，后续需要凑出来的余数  
             int need = (k + r - (grid[i][j] % k)) % k;  
             int ans = 0;  
             //向下走  
             if (i + 1 < n) {  
                 ans = f1(grid, n, m, k, i + 1, j, need);  
             }  
             //向右走  
             if (j + 1 < m) {  
                 ans = (ans + f1(grid, n, m, k, i, j + 1, need)) % MOD;  
             }  
             return ans;  
         }  
   
         /**  
          记忆化搜索  
          */  
         public static int numberOfPaths2(int[][] grid, int k) {  
             int n = grid.length;  
             int m = grid[0].length;  
             int[][][] dp = new int[n + 1][m + 1][k + 1];  
             for (int i = 0; i <= n; i++) {  
                 for (int j = 0; j <= m; j++) {  
                     for (int c = 0; c <= k; c++) {  
                         dp[i][j][c] = -1;  
                     }  
                 }  
             }  
             return f2(grid, n, m, k, 0, 0, 0, dp);  
         }  
   
         /**  
          从(i,j)位置到目标点（n-1,m-1）有多少条路径，累和整除k的余数是r  
          */        public static int f2(int[][] grid, int n, int m, int k, int i, int j, int r, int[][][] dp) {  
             if (i == n - 1 && j == m - 1) {  
                 return grid[i][j] % k == r ? 1 : 0;  
             }  
             if (dp[i][j][r] != -1) {  
                 return dp[i][j][r];  
             }  
             //累和当前点后，接着向目标点出发，后续需要凑出来的余数  
             int need = (k + r - (grid[i][j] % k)) % k;  
             int ans = 0;  
             //向下走  
             if (i + 1 < n) {  
                 ans = f2(grid, n, m, k, i + 1, j, need, dp);  
             }  
             //向右走  
             if (j + 1 < m) {  
                 ans = (ans + f2(grid, n, m, k, i, j + 1, need, dp)) % MOD;  
             }  
             dp[i][j][r] = ans;  
             return ans;  
         }  
   
         /**  
          严格按照位置的动态规划  
          */  
         public static int numberOfPaths3(int[][] grid, int k) {  
             int n = grid.length;  
             int m = grid[0].length;  
             int[][][] dp = new int[n + 1][m + 1][k + 1];  
             for (int c = 0; c <= k; c++) {  
                 if ((grid[n - 1][m - 1]) % k == c) {  
                     dp[n - 1][m - 1][c] = 1;  
                 }  
             }  
             for (int i = n - 1; i >= 0; i--) {  
                 for (int j = m - 1; j >= 0; j--) {  
                     for (int c = k; c >= 0; c--) {  
                         int need = (k + c - (grid[i][j] % k)) % k;  
                         if (i + 1 < n) {  
                             dp[i][j][c] = dp[i + 1][j][need];  
                         }  
                         if (j + 1 < m) {  
                             dp[i][j][c] = (dp[i][j][c] +dp[i][j+1][need]) % MOD;  
                         }  
                     }  
                 }  
             }  
             return dp[0][0][0];  
         }  
     }  
 }

5、扰乱字符串

题目描述：使用下面描述的算法可以扰乱字符串 s 得到字符串 t ：

如果字符串的长度为 1 ，算法停止
如果字符串的长度 > 1 ，执行下述步骤：
- 在一个随机下标处将字符串分割成两个非空的子字符串。即，如果已知字符串 s ，则可以将其分成两个子字符串 x 和 y ，且满足 s = x + y 。
- 随机决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即，在执行这一步骤之后，s 可能是 s = x + y 或者 s = y + x 。
- 在 x 和 y 这两个子字符串上继续从步骤 1 开始递归执行此算法。

给你两个 长度相等 的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：s1 = "great", s2 = "rgeat" 输出：true 解释：s1 上可能发生的一种情形是： "great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串 "gr/eat" --> "gr/eat" // 随机决定：「保持这两个子字符串的顺序不变」 "gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割 "g/r / e/at" --> "r/g / e/at" // 随机决定：第一组「交换两个子字符串」，第二组「保持这两个子字符串的顺序不变」 "r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法，将 "at" 分割得到 "a/t" "r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定：「保持这两个子字符串的顺序不变」算法终止，结果字符串和 s2 相同，都是 "rgeat" 这是一种能够扰乱 s1 得到 s2 的情形，可以认为 s2 是 s1 的扰乱字符串，返回 true

示例 2：

输入：s1 = "abcde", s2 = "caebd" 输出：false

示例 3：

输入：s1 = "a", s2 = "a" 输出：true

提示：

s1.length == s2.length
1 <= s1.length <= 30
s1 和 s2 由小写英文字母组成

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 87 - Scramble String（扰乱字符串）
🧠 题目关键词（原文关键词）	递归分割、交换/不交换、子串、记忆化、区间 DP、字符频次剪枝
🧩 抽象问题类型（题目本质）	区间划分 + 二叉递归结构判定（等价于判断两串是否同一二叉划分树的同构；可用记忆化 DFS 或 3D DP）
🔍 数据规模 / 限制	1 ≤ n ≤ 30；暴力指数级，需要强剪枝 + 记忆化；记忆化 DFS 典型复杂度约 O(n³)（含每层 O(n) 分割与 O(n) 频次比较）
🧭 我的初步思路	完全没思路
✅ 正确解法类型	记忆化 DFS（哈希表/三元键 i,j,len） + 频次剪枝（排序/计数）；或 DPl[j]（长度为 l、起点 i 与 j 的子串是否可扰乱）
❗ 没想到的原因	未做字符多重集合一致性剪枝导致 TLE；或记忆化维度不对（漏掉长度/起点），或把“交换/不交换”两种情况漏判
📦 归入的题型分类	区间/划分类、递归与记忆化、字符串判定类
🧠 触发词（以后遇到就联想）	“把串分成两半递归 + 可交换顺序/不交换 + 判定同构” → 记忆化 DFS / 区间 DP
🧪 解法一句话总结	设 `f(i,j,len)`：`s1[i..i+len)` 与 `s2[j..j+len)` 是否可扰乱；若两段字符频次不同直接 false，否则枚举分割 `k`，检查 `(f(i,j,k)&&f(i+k,j+k,len-k))

这个题哪怕到记忆化搜索都过不了，只能严格依赖位置的动态规划才能过。

 package main.java.class069;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code05_ScrambleString  
  * @description: 扰乱字符串  
  * // 使用下面描述的算法可以扰乱字符串 s 得到字符串 t ：  
  * // 步骤1 : 如果字符串的长度为 1 ，算法停止  
  * // 步骤2 : 如果字符串的长度 > 1 ，执行下述步骤：  
  * //        在一个随机下标处将字符串分割成两个非空的子字符串  
  * //        已知字符串s，则可以将其分成两个子字符串x和y且满足s=x+y  
  * //        可以决定是要 交换两个子字符串 还是要 保持这两个子字符串的顺序不变  
  * //        即s可能是 s = x + y 或者 s = y + x  
  * //        在x和y这两个子字符串上继续从步骤1开始递归执行此算法  
  * // 给你两个 长度相等 的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串  
  * // 如果是，返回true ；否则，返回false  
  * // 测试链接 : https://leetcode.cn/problems/scramble-string/  
  * @author: zs宝  
  * @create: 2025-08-17 10:54  
  * @Version 1.0  
  **/public class Code05_ScrambleString {  
     class Solution {  
         public boolean isScramble(String s1, String s2) {  
             return isScramble4(s1, s2);  
         }  
   
         /**  
          暴力递归的尝试  
          */  
         public boolean isScramble1(String str1, String str2) {  
             char[] s1 = str1.toCharArray();  
             char[] s2 = str2.toCharArray();  
             int n = s1.length;  
             return f1(s1, 0, n - 1, s2, 0, n - 1);  
         }  
   
         /**  
          s2[l2,r2]是否是s1[l1,r1]的扰乱串，要等长度  
          */  
         public boolean f1(char[] s1, int l1, int r1, char[] s2, int l2, int r2) {  
             if (l1 == r1) {  
                 return s1[l1] == s2[l2];  
             }  
             // s1[l1..i][i+1....r1]  
             // s2[l2..j][j+1....r2]            // 不交错去讨论扰乱关系  
             for (int i = l1, j = l2; i < r1 && j < r2; i++, j++) {  
                 if (f1(s1, l1, i, s2, l2, j) & f1(s1, i + 1, r1, s2, j + 1, r2)) {  
                     return true;  
                 }  
             }  
             // s1[l1..i][i+1....r1]  
             // s2[j+1....r2][l2..j]            // 交错的去讨论扰乱关系  
             for (int i = l1, j = r2; i < r1 && j > l2; i++, j--) {  
                 if (f1(s1, l1, i, s2, j, r2) & f1(s1, i + 1, r1, s2, l2, j - 1)) {  
                     return true;  
                 }  
             }  
   
             return false;  
         }  
   
         /**  
          优化的暴力递归：参数量减少,四个可变参数，变成了三个  
          */  
         public boolean isScramble2(String str1, String str2) {  
             char[] s1 = str1.toCharArray();  
             char[] s2 = str2.toCharArray();  
             int n = s1.length;  
             return f2(s1, s2, 0, 0, n);  
         }  
   
         /**  
          s2[l2,r2]是否是s1[l1,r1]的扰乱串，要等长度  
          */  
         public boolean f2(char[] s1, char[] s2, int l1, int l2, int len) {  
             if (len == 1) {  
                 return s1[l1] == s2[l2];  
             }  
             // s1[l1..i][i+1....r1]  
             // s2[l2..j][j+1....r2]            // 不交错去讨论扰乱关系  
             for (int k = 1; k < len; k++) {  
                 if (f2(s1, s2, l1, l2, k) & f2(s1, s2, l1 + k, l2 + k, len - k)) {  
                     return true;  
                 }  
             }  
             // s1[l1..i][i+1....r1]  
             // s2[j+1....r2][l2..j]            // 交错的去讨论扰乱关系  
             for (int i = l1 + 1, j = l2 + len - 1, k = 1; k < len; i++, j--, k++) {  
                 if (f2(s1, s2, l1, j, k) & f2(s1, s2, i, l2, len - k)) {  
                     return true;  
                 }  
             }  
             return false;  
         }  
   
         /**  
          记忆化搜索：由暴力递归优化而来，仍然超时，但是比暴力递归通过的测试用例更多  
          */  
         public boolean isScramble3(String str1, String str2) {  
             char[] s1 = str1.toCharArray();  
             char[] s2 = str2.toCharArray();  
             int n = s1.length;  
             int[][][] dp = new int[n][n][n + 1];  
             return f3(s1, s2, 0, 0, n, dp);  
         }  
   
         /**  
          s2[l2,r2]是否是s1[l1,r1]的扰乱串，要等长度  
          */  
         public boolean f3(char[] s1, char[] s2, int l1, int l2, int len, int[][][] dp) {  
             if (len == 1) {  
                 return s1[l1] == s2[l2];  
             }  
             if (dp[l1][l2][len] != 0) {  
                 return dp[l1][l2][len] == 1;  
             }  
             boolean ans = false;  
             // s1[l1..i][i+1....r1]  
             // s2[l2..j][j+1....r2]            // 不交错去讨论扰乱关系  
             for (int k = 1; k < len; k++) {  
                 if (f3(s1, s2, l1, l2, k, dp) && f3(s1, s2, l1 + k, l2 + k, len - k, dp)) {  
                     ans = true;  
                     break;  
                 }  
             }  
             // s1[l1..i][i+1....r1]  
             // s2[j+1....r2][l2..j]            // 交错的去讨论扰乱关系  
             if (!ans) {  
                 for (int i = l1 + 1, j = l2 + len - 1, k = 1; k < len; i++, j--, k++) {  
                     if (f3(s1, s2, l1, j, k, dp) && f3(s1, s2, i, l2, len - k, dp)) {  
                         ans = true;  
                         break;  
                     }  
                 }  
             }  
   
             dp[l1][l2][len] = ans ? 1 : 0;  
             return ans;  
         }  
   
         /**  
          严格依赖位置的动态规划：由记忆化搜索优化而来  
          */  
         public boolean isScramble4(String str1, String str2) {  
             char[] s1 = str1.toCharArray();  
             char[] s2 = str2.toCharArray();  
             int n = s1.length;  
             boolean[][][] dp = new boolean[n][n][n + 1];  
             //填写长度为1的格子  
             for (int l1 = 0; l1 < n; l1++) {  
                 for (int l2 = 0; l2 < n; l2++) {  
                     dp[l1][l2][1] = s1[l1] == s2[l2];  
                 }  
             }  
             for (int len = 2; len <=n; len++) {  
                 for (int l1 = 0; l1 <= n - len; l1++) {  
                     for (int l2 = 0; l2 <= n - len; l2++) {  
                         for(int k=1;k<len;k++){  
                             //不交错  
                             if(dp[l1][l2][k] && dp[l1+k][l2+k][len-k]){  
                                 dp[l1][l2][len] = true;  
                                 break;  
                             }  
                         }  
                         if(!dp[l1][l2][len]){  
                             for(int i = l1 + 1, j = l2 + len - 1, k = 1; k < len; i++, j--, k++){  
                                 if(dp[l1][j][k] && dp[i][l2][len-k]){  
                                     dp[l1][l2][len] = true;  
                                     break;  
                                 }  
                             }  
                         }  
                     }  
                 }  
             }  
             return dp[0][0][n];  
         }  
     }  
 }

参考资料

左程云-算法通关系列-069

如果觉得文章对你有用，请随意赞赏

算法动态规划

动态规划04：从递归入手三维动态规划

https://zshunbao.top/archives/dong-tai-gui-hua-04-cong-di-gui-ru-shou-san-wei-dong-tai-gui-hua

作者

zs宝

发布于

2025-08-17

更新于

2025-08-17

许可协议

CC BY 4.0