核心思想
分组背包:多个物品分组,每组只能取1件 每一组的物品都可能性展开就可以了。注意时间复杂度不会升阶,O (物品数量 * 背包容量)
完全背包:与01背包的区别仅在于 每种商品可以选取无限次。时间复杂度O (物品数量 * 背包容量)
例题
1、分组背包模版
题目描述: 给定一个正数m表示背包的容量,有n个货物可供挑选 每个货物有自己的体积 (容量消耗)、价值 (获得收益)、组号 (分组) 同一个组的物品只能挑选1件,所有挑选物品的体积总和不能超过背包容量 怎么挑选货物能达到价值最大,返回最大的价值

解题思路:
这里是一个典型的分组背包问题,在01背包基础上挤上来分组的概念,每个分组只允许拿一件商品
那么这里的 dp [ i ] [ j ] 定义为在1-i组上,每个组的物品挑一件,挑选物品的体积不超过j所能带来的最大价值
不要第i组的商品--dp [i] [j]=dp[i-1] [j]
要第i组的商铺,那么i组的每个商品都要进行尝试,找出最大价值
代码如下:
package main.java.class074;
import java.io.*;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code01_PartitionedKnapsack
* @description: 分组背包(模版)
* // 给定一个正数m表示背包的容量,有n个货物可供挑选
* // 每个货物有自己的体积(容量消耗)、价值(获得收益)、组号(分组)
* // 同一个组的物品只能挑选1件,所有挑选物品的体积总和不能超过背包容量
* // 怎么挑选货物能达到价值最大,返回最大的价值
* // 测试链接 : https://www.luogu.com.cn/problem/P1757
* @author: zs宝
* @create: 2025-09-04 09:30
* @Version 1.0
**/public class Code01_PartitionedKnapsack {
public static int MAXM=1001;
public static int MAXN=1001;
public static int m,n;
public static int[][]arr=new int[MAXN][3];
public static int[]dp=new int[MAXM];
public static void main(String[] args) throws IOException {
BufferedReader buffer=new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in=new StreamTokenizer(buffer);
PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken()!=StreamTokenizer.TT_EOF){
m=(int)in.nval;
in.nextToken();
n=(int)in.nval;
for(int i=1;i<=n;i++){
in.nextToken();
arr[i][0]=(int)in.nval;
in.nextToken();
arr[i][1]=(int)in.nval;
in.nextToken();
arr[i][2]=(int)in.nval;
}
Arrays.sort(arr,1,n+1,(a,b)->a[2]-b[2]);
out.println(compute1());
}
out.flush();
out.close();
buffer.close();
}
//严格以案例位置的动态规划
public static int compute1(){
//首先查清楚给定数据究竟有多少组
int teams=1;
for(int i=2;i<=n;i++){
if(arr[i][2]!=arr[i-1][2]){
teams++;
}
}
//dp[i][j]:在1-i组上,每个组的物品挑一件,挑选物品的体积不超过j所能带来的最大价值
int[][]dp=new int[teams+1][m+1];
for(int start=1,end=2,i=1;start<=n;i++){
//首先确定当前组在arr数组上的范围
while (end<=n && arr[end][2]==arr[start][2]){
end++;
}
//接下来对每个容量进行遍历
for(int j=0;j<=m;j++){
//当不选当前组的商铺时,最大价值为
dp[i][j]=dp[i-1][j];
//接下来,遍历选择当前组的商品进行求解,但是只能选一件,
for(int k=start;k<end;k++){
if(j-arr[k][0]>=0){
dp[i][j]=Math.max(dp[i][j],dp[i-1][j-arr[k][0]]+arr[k][1]);
}
}
}
start=end++;
}
return dp[teams][m];
}
//严格按照位置依赖的动态规划+空间压缩
public static int compute2(){
Arrays.fill(dp,0,m+1,0);
for(int start=1,end=2,i=1;start<=n;i++){
//首先确定当前组在arr数组上的范围
while (end<=n && arr[end][2]==arr[start][2]){
end++;
}
//接下来对每个容量进行遍历
for(int j=m;j>=0;j--){
//接下来,遍历选择当前组的商品进行求解,但是只能选一件,
for(int k=start;k<end;k++){
if(j-arr[k][0]>=0){
dp[j]=Math.max(dp[j],dp[j-arr[k][0]]+arr[k][1]);
}
}
}
start=end++;
}
return dp[m];
}
}2、从栈中取出K个硬币的最大面值和
题目描述: 一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币。
每一次操作中,你可以从任意一个栈的 顶部 取出 1 个硬币,从栈中移除它,并放入你的钱包里。
给你一个列表 piles ,其中 piles[i] 是一个整数数组,分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ,请你返回在 恰好 进行 k 次操作的前提下,你钱包里硬币面值之和 最大为多少 。
示例 1:
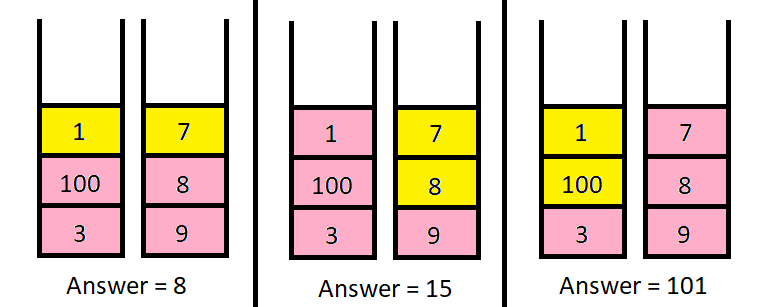
输入:piles = [[1,100,3],[7,8,9]], k = 2 输出:101 解释: 上图展示了几种选择 k 个硬币的不同方法。 我们可以得到的最大面值为 101 。
示例 2:
输入:piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7 输出:706 解释: 如果我们所有硬币都从最后一个栈中取,可以得到最大面值和。
提示:
n == piles.length1 <= n <= 10001 <= piles[i][j] <= 1051 <= k <= sum(piles[i].length) <= 2000
解题思路:
这个题说实话还真不容易将其转化为分组背包,当看到可以在同一个栈中不断拿硬币时很容易把它当成完全背包问题,但其实并不是
这个难点就在于如何将其转化为分组背包,而大多数考分组背包问题的题,真正的难点不在于其代码,而在于转化为分组背包的思路上面
转化思路如下
总共有多少个栈,就代表有多少个分组
每次只能在分组中拿一个物品,但是这里的物品不再指的是一个硬币这种,而是将一种方案当成一个物品,比如在当前栈内拿3个硬币这是一种方案,在当前栈内拿5个硬笔这也是一种方案。
dp[i] [j]定义为1~i组上,一共拿走j个硬币的情况下,获得的最大价值
代码如下:
package main.java.class074;
import java.util.List;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code02_MaximumValueOfKcoinsFromPiles
* @description: 从栈中取出K个硬币的最大面值和
* // 一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币
* // 每一次操作中,你可以从任意一个栈的 顶部 取出 1 个硬币,从栈中移除它,并放入你的钱包里
* // 给你一个列表 piles ,其中 piles[i] 是一个整数数组
* // 分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k
* // 请你返回在 恰好 进行 k 次操作的前提下,你钱包里硬币面值之和 最大为多少
* // 测试链接 : https://leetcode.cn/problems/maximum-value-of-k-coins-from-piles/
* @author: zs宝
* @create: 2025-09-04 10:27
* @Version 1.0
**/public class Code02_MaximumValueOfKcoinsFromPiles {
class Solution {
public int maxValueOfCoins(List<List<Integer>> piles, int k) {
return maxValueOfCoins2(piles,k);
}
/**
严格按照位置依赖的动态规划
// piles是一组一组的硬币
// m是容量,表示一定要进行m次操作
// dp[i][j] : 1~i组上,一共拿走j个硬币的情况下,获得的最大价值
// 1) 不要i组的硬币 : dp[i-1][j]
// 2) i组里尝试每一种方案,把一种方案当作一种物品
// 比如,i组里拿走前k个硬币的方案 : dp[i-1][j-k] + 从顶部开始前k个硬币的价值和
// 枚举每一个k,选出最大值
*/
public int maxValueOfCoins1(List<List<Integer>> piles, int m) {
int n=piles.size();
int[][]dp=new int[n+1][m+1];
for(int i=1;i<=n;i++){
//获得当前栈
List<Integer>team=piles.get(i-1);
int t=Math.min(m,team.size());
//构造前缀和加速计算
//由于是将方案当作一个物品,这个方案可能拿前面的几个硬币,因此每种前缀和就对应着一种方案
int[]preSum=new int[t+1];
for(int k=0,sum=0;k<t;k++){
sum+=team.get(k);
preSum[k+1]=sum;
}
//更新动态规划表
for(int j=0;j<=m;j++){
//不拿走当前分组硬币
dp[i][j]=dp[i-1][j];
//每次操作拿走当前组硬币
//将每次在一组内拿走多少硬币的方案当作物品,而不是一个拿走一个硬币当作物品
//拿走都少呢
for(int k=1;k<=Math.min(t,j);k++){
dp[i][j]=Math.max(dp[i][j],dp[i-1][j-k]+preSum[k]);
}
}
}
return dp[n][m];
}
/**
严格按照位置依赖的动态规划+空间压缩
*/
public int maxValueOfCoins2(List<List<Integer>> piles, int m) {
int n=piles.size();
int[]dp=new int[m+1];
for(int i=1;i<=n;i++){
//获得当前栈
List<Integer>team=piles.get(i-1);
int t=Math.min(m,team.size());
//构造前缀和加速计算
int[]preSum=new int[t+1];
for(int k=0,sum=0;k<t;k++){
sum+=team.get(k);
preSum[k+1]=sum;
}
//更新动态规划表
for(int j=m;j>=0;j--){
//不拿走当前分组硬币
//dp[j]=dp[i-1][j];
//每次操作拿走当前组硬币
//拿走都少呢
for(int k=1;k<=Math.min(t,j);k++){
dp[j]=Math.max(dp[j],dp[j-k]+preSum[k]);
}
}
}
return dp[m];
}
}
}3、完全背包 (模版)
给定一个正数t,表示背包的容量 有m种货物,每种货物可以选择任意个 每种货物都有体积costs[i]和价值values[i] 返回在不超过总容量的情况下,怎么挑选货物能达到价值最大 返回最大的价值

解题思路:
这是一个完全背包问题的模版题,完全背包不同于之前学习的所有背包处在于,完全背包的所有物品可以无限拿
除了无限拿,其余几乎与01背包没有差别
定义dp[i] [j]为:前1-i种物品随便取,在j容量内可以采集到的最大价值
无限拿的具体体现在
dp[i][j] = Math.max (dp[i][j], dp[i][j - arr[i][0]] + arr[i][1]);其中是dp[i][j - arr[i][0]] + arr[i][1])是dp[i] [...]以往都是dp[i-1][....]
代码如下
package main.java.class074;
import java.io.*;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code03_UnboundedKnapsack
* @description: 完全背包(模版)
* // 给定一个正数t,表示背包的容量
* // 有m种货物,每种货物可以选择任意个
* // 每种货物都有体积costs[i]和价值values[i]
* // 返回在不超过总容量的情况下,怎么挑选货物能达到价值最大
* // 返回最大的价值
* // 测试链接 : https://www.luogu.com.cn/problem/P1616
* @author: zs宝
* @create: 2025-09-05 09:13
* @Version 1.0
**/public class Code03_UnboundedKnapsack {
public static int MAXM = 10001;
public static int MAXT = 10000001;
public static int[][] arr = new int[MAXM][2];
public static int m, t;
public static long[] dp = new long[MAXT];
public static void main(String[] args) throws IOException {
BufferedReader buffer = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(buffer);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
t = (int) in.nval;
in.nextToken();
m = (int) in.nval;
for (int i = 1; i <= m; i++) {
in.nextToken();
arr[i][0] = (int) in.nval;
in.nextToken();
arr[i][1] = (int) in.nval;
}
out.println(compute2());
}
out.flush();
out.close();
buffer.close();
}
//严格依赖位置的动态规划
public static long compute1() {
//dp[i][j]:前1-i种物品随便取,在t时间内可以采集到的最大价值
int[][] dp = new int[m + 1][t + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= t; j++) {
//不采集第i中物品
dp[i][j] = dp[i - 1][j];
if (j - arr[i][0] >= 0) {
//注意这里是dp[i][j-arr[i][0]]+arr[i][1],而不是dp[i-1][j-arr[i][0]]+arr[i][1]
//这就与以往的背包问题不同,表明1-i可以无限取
dp[i][j] = Math.max(dp[i][j], dp[i][j - arr[i][0]] + arr[i][1]);
}
}
}
return dp[m][t];
}
//严格依赖位置的动态规划+空间压缩
public static long compute2() {
Arrays.fill(dp, 0, t + 1, 0);
for (int i = 1; i <= m; i++) {
for (int j = arr[i][0]; j<=t ; j++) {
//注意这里是dp[i][j-arr[i][0]]+arr[i][1],而不是dp[i-1][j-arr[i][0]]+arr[i][1]
//这就与以往的背包问题不同,表明1-i可以无限取
dp[j] = Math.max(dp[j], dp[j - arr[i][0]] + arr[i][1]);
}
}
return dp[t];
}
}4、正则表达式匹配
题目描述: 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s 的,而不是部分字符串。
示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa", p = "a" 输出:true 解释:因为 '' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab", p = "." 输出:true 解释:"." 表示可匹配零个或多个('*')任意字符('.')。
提示:
1 <= s.length <= 201 <= p.length <= 20s只包含从a-z的小写字母。p只包含从a-z的小写字母,以及字符.和*。保证每次出现字符
*时,前面都匹配到有效的字符
解题思路:
这道题的难点在于分类讨论的复杂,很有可能情况不全
详细的讨论请看代码注释
代码如下
package main.java.class074;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code04_RegularExpressionMatching
* @description: 正则表达式匹配
* // 给你字符串s、字符串p
* // s中一定不含有'.'、'*'字符,p中可能含有'.'、'*'字符
* // '.' 表示可以变成任意字符,数量1个
* // '*' 表示可以让 '*' 前面那个字符数量任意(甚至可以是0个)
* // p中即便有'*',一定不会出现以'*'开头的情况,也一定不会出现多个'*'相邻的情况(无意义)
* // 请实现一个支持 '.' 和 '*' 的正则表达式匹配
* // 返回p的整个字符串能不能匹配出s的整个字符串
* // 测试链接 : https://leetcode.cn/problems/regular-expression-matching/
* @author: zs宝
* @create: 2025-09-05 09:47
* @Version 1.0
**/public class Code04_RegularExpressionMatching {
class Solution {
public boolean isMatch(String str, String par) {
return isMatch3(str, par);
}
/**
纯暴力递归解法
*/
public boolean isMatch1(String str, String par) {
char[] s = str.toCharArray();
char[] p = par.toCharArray();
return f1(s, p, 0, 0);
}
/**
递归:难点在于分类讨论齐全
*/
public boolean f1(char[] s, char[] p, int i, int j) {
//当s遍历完,而p还没有遍历完时
if (i == s.length) {
//s,p都遍历完时
if (j == p.length) {
return true;
} else {
//s遍历完,而p为遍历完
//这个点,p后面如果还有字符
//能返回true的唯一情况就是下一个字符j+1为*,这样当前j多的字符就都能够删减掉
return j + 1 < p.length && p[j + 1] == '*' && f1(s, p, i, j + 2);
}
} else if (j == p.length) {
//当s未遍历完,而p遍历完时
return false;
} else {
//当s,p都没有遍历完时
//这个时候当前p的字符可能时字母,.,*
//但是对于*是无法单独进行匹配的,因此我们将*当作一种附属,只有讨论字母或者.的时候,且下一个位置为*,
//这个才有意义
//因此我们不单独讨论j指向*的情况,每当遇到字母或者.时判断下一个字符是否为*,进行分类讨论
//还有一个原因就是,如果单独讨论*,那么就一定会涉及到j-1的字符,但是前面j-1的字符已经匹配涉及到了
//如果j-1的字符不等于i位置的字符,*只能选择让前面为0,那么这个时候前面j位置以前匹配过的情况就要重新计算
//这样相当于从j有回退的情况,这与我们递归的一直从0,0开始往后走,方向上不对,增加讨论的复杂度
//换个思考方式进行讨论容易清晰很多
//当当前字符后面一个字符不是*时,或者当前字符为p的最后一个字符
if (j + 1 == p.length || p[j + 1] != '*') {
return (p[j] == '.' || p[j] == s[i]) && f1(s, p, i + 1, j + 1);
} else {
//当当前j字符的下一个字符是*时,即p[j+1]=='*'
//若当前j字符匹配不了i位置的字符,后面的*直接情空当前位置
boolean p1 = f1(s, p, i, j + 2);
//若当前j位置的字符匹配的了i位置的字符
//完全背包,j+1位置的*可以让让j位置的字符边多个,到底要几个呢,就看i+1位置的是否和j位置同,无限拿
boolean p2 = (p[j] == s[i] || p[j] == '.') && f1(s, p, i + 1, j);
return p1 || p2;
}
}
}
/**
记忆化搜索:由暴力递归优化而来
*/
public boolean isMatch2(String str, String par) {
char[] s = str.toCharArray();
char[] p = par.toCharArray();
//dp[i][j]:s[0,i-1]位置与p[0,j-1]位置的匹配情况
//0表示为匹配过,1表示匹配争取,2表示匹配失败
int[][] dp = new int[s.length + 1][p.length + 1];
return f2(s, p, 0, 0, dp);
}
/**
递归:难点在于分类讨论齐全
*/
public boolean f2(char[] s, char[] p, int i, int j, int[][] dp) {
if (dp[i][j] != 0) {
return dp[i][j] == 1;
}
boolean ans;
//当s遍历完,而p还没有遍历完时
if (i == s.length) {
//s,p都遍历完时
if (j == p.length) {
ans = true;
} else {
//s遍历完,而p为遍历完
//这个点,p后面如果还有字符
//能返回true的唯一情况就是下一个字符j+1为*,这样当前j多的字符就都能够删减掉
ans = j + 1 < p.length && p[j + 1] == '*' && f2(s, p, i, j + 2, dp);
}
} else if (j == p.length) {
//当s未遍历完,而p遍历完时
ans = false;
} else {
//当s,p都没有遍历完时
//这个时候当前p的字符可能时字母,.,*
//但是对于*是无法单独进行匹配的,因此我们将*当作一种附属,只有讨论字母或者.的时候,且下一个位置为*,
//这个才有意义
//因此我们不单独讨论j指向*的情况,每当遇到字母或者.时判断下一个字符是否为*,进行分类讨论
//还有一个原因就是,如果单独讨论*,那么就一定会涉及到j-1的字符,但是前面j-1的字符已经匹配涉及到了
//如果j-1的字符不等于i位置的字符,*只能选择让前面为0,那么这个时候前面j位置以前匹配过的情况就要重新计算
//这样相当于从j有回退的情况,这与我们递归的一直从0,0开始往后走,方向上不对,增加讨论的复杂度
//换个思考方式进行讨论容易清晰很多
//当当前字符后面一个字符不是*时,或者当前字符为p的最后一个字符
if (j + 1 == p.length || p[j + 1] != '*') {
ans = (p[j] == '.' || p[j] == s[i]) && f2(s, p, i + 1, j + 1, dp);
} else {
//当当前j字符的下一个字符是*时,即p[j+1]=='*'
//若当前j字符匹配不了i位置的字符,后面的*直接情空当前位置
boolean p1 = f2(s, p, i, j + 2, dp);
//若当前j位置的字符匹配的了i位置的字符
//完全背包,j+1位置的*可以让让j位置的字符边多个,到底要几个呢,就看i+1位置的是否和j位置同,无限拿
boolean p2 = (p[j] == s[i] || p[j] == '.') && f2(s, p, i + 1, j, dp);
ans = p1 || p2;
}
}
dp[i][j] = ans ? 1 : 2;
return ans;
}
/**
严格按照位置依赖的动态规划
//直接根据之前讨论的分类依次填值
*/
public boolean isMatch3(String str, String par) {
char[] s = str.toCharArray();
char[] p = par.toCharArray();
int n = s.length;
int m = p.length;
//dp[i][j]:s[0,i-1]位置与p[0,j-1]位置的匹配情况
//0表示为匹配过,1表示匹配争取,2表示匹配失败
//初始值默认为false
boolean[][] dp = new boolean[n + 1][m + 1];
//直接根据之前讨论的分类依次填值
//i==s.length && j==p.length时
dp[n][m] = true;
//i==s.length ,j!=p.length时
//ans= j+1<p.length && p[j+1]=='*' && f2(s,p,i,j+2,dp);
for (int j = m - 1; j >= 0; j--) {
dp[n][j] = j + 1 < m && p[j + 1] == '*' && dp[n][j + 2];
}
//i!=s.length ,j==p.length时,全部为false,而dp初始值默认为false
//当s,p都没有遍历完时
for (int i = n - 1; i >= 0; i--) {
for (int j = m - 1; j >= 0; j--) {
if (j + 1 == m || p[j + 1] != '*') {
dp[i][j] = (p[j] == '.' || p[j] == s[i]) && dp[i+1][j+1];
} else {
//当当前j字符的下一个字符是*时,即p[j+1]=='*'
//若当前j字符匹配不了i位置的字符,后面的*直接情空当前位置
boolean p1 = dp[i][j+2];
//若当前j位置的字符匹配的了i位置的字符
//完全背包,j+1位置的*可以让让j位置的字符边多个,到底要几个呢,就看i+1位置的是否和j位置同,无限拿
boolean p2 = (p[j] == s[i] || p[j] == '.') && dp[i+1][j];
dp[i][j] = p1 || p2;
}
}
}
return dp[0][0];
}
}
}5、 通配符匹配
题目描述: 给你一个输入字符串 (s) 和一个字符模式 (p) ,请你实现一个支持 '?' 和 '*' 匹配规则的通配符匹配:
'?'可以匹配任何单个字符。'*'可以匹配任意字符序列(包括空字符序列)。
判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。
示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa", p = "" 输出:true 解释:'' 可以匹配任意字符串。
示例 3:
输入:s = "cb", p = "?a" 输出:false 解释:'?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。
提示:
0 <= s.length, p.length <= 2000s仅由小写英文字母组成p仅由小写英文字母、'?'或'*'组成
解题思路:
这个题与第4个题十分类似, 甚至分类讨论还更简单一点
但是我还是在最后对
'*'的那部分讨论错误了我最开始想到的是,在j位置的* 由于它可以变成任意子串,那么这个时候我就要考虑j位置后面还有多少字符,那么如果要匹配,s中至少要由足量字符,所以我直接跳过* 开始去匹配p剩余最后字符与s中末尾等量的字符
但是上述考虑只想到了s中后续字符长度长于p的后续长度的情况,也有可能s后续长度小于p的后续,并且将情况想复杂了
在j位置的* 只需要考虑这个* 需不需要去匹配当前字符,匹配了也可以匹配后续的字符,不匹配就是让它变空,这样的二叉树形式让它往下递归就可以了,不需要想的特别复杂
代码
package main.java.class074;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code05_WildcardMatching
* @description: 通配符匹配(和题目4高度相似,只是边界条件不同而已,而且更简单)
* // 给你字符串s、字符串p
* // s中一定不含有'?'、'*'字符,p中可能含有'?'、'*'字符
* // '?' 表示可以变成任意字符,数量1个
* // '*' 表示可以匹配任何字符串
* // 请实现一个支持 '?' 和 '*' 的通配符匹配
* // 返回p的整个字符串能不能匹配出s的整个字符串
* // 测试链接 : https://leetcode.cn/problems/wildcard-matching/
* @author: zs宝
* @create: 2025-09-06 14:17
* @Version 1.0
**/public class Code05_WildcardMatching {
class Solution {
public boolean isMatch(String s, String p) {
return isMatch3(s, p);
}
/**
暴力递归
*/
public boolean isMatch1(String str, String par) {
char[] s = str.toCharArray();
char[] p = par.toCharArray();
return f1(s, p, 0, 0);
}
public boolean f1(char[] s, char[] p, int i, int j) {
//当s遍历完,
if (i == s.length) {
//若p也遍历完了
if (j == p.length) {
return true;
} else {
// 如果p[j]是*,可以消掉,然后看看p[j+1....]是不是都能消掉
return p[j] == '*' && f1(s, p, i, j + 1);
}
} else if (j == p.length) {
//当s未遍历完,p遍历完
return false;
} else {
if(p[j]!='*'){
return (p[j]=='?' || p[j]==s[i]) && f1(s,p,i+1,j+1);
}else{
//选择让当前的*搞定i位置
//或者不让当前的*搞定i位置
return f1(s,p,i+1,j) || f1(s,p,i,j+1);
}
}
}
/**
记忆化搜索
*/
public boolean isMatch2(String str, String par) {
char[] s = str.toCharArray();
char[] p = par.toCharArray();
//dp[i][j]:s[0,i-1]与p[0,i-1]的匹配状况
//0:表示未进行匹配,1表示匹配成功,2表示匹配成功
int[][]dp=new int[s.length+1][p.length+1];
return f2(s, p, 0, 0,dp);
}
public boolean f2(char[] s, char[] p, int i, int j,int[][]dp) {
if(dp[i][j]!=0){
return dp[i][j]==1;
}
boolean ans;
//当s遍历完,
if (i == s.length) {
//若p也遍历完了
if (j == p.length) {
ans= true;
} else {
// 如果p[j]是*,可以消掉,然后看看p[j+1....]是不是都能消掉
ans= p[j] == '*' && f2(s, p, i, j + 1,dp);
}
} else if (j == p.length) {
//当s未遍历完,p遍历完
ans= false;
} else {
if(p[j]!='*'){
ans= (p[j]=='?' || p[j]==s[i]) && f2(s,p,i+1,j+1,dp);
}else{
//选择让当前的*搞定i位置
//或者不让当前的*搞定i位置
ans= f2(s,p,i+1,j,dp) || f2(s,p,i,j+1,dp);
}
}
dp[i][j]=ans?1:2;
return ans;
}
/**
严格依赖位置的动态规划
*/
public boolean isMatch3(String str, String par) {
char[] s = str.toCharArray();
char[] p = par.toCharArray();
int n=s.length;
int m=p.length;
//dp[i][j]:s[0,i-1]与p[0,i-1]的匹配状况
//0:表示未进行匹配,1表示匹配成功,2表示匹配成功
boolean[][]dp=new boolean[n+1][m+1];
dp[n][m]=true;
for(int j=m-1;j>=0;j--){
dp[n][j]=p[j] == '*' && dp[n][j+1];
}
for(int i=n-1;i>=0;i--){
for(int j=m-1;j>=0;j--){
if(p[j]!='*'){
dp[i][j]= (p[j]=='?' || p[j]==s[i]) && dp[i+1][j+1];
}else{
dp[i][j]= dp[i+1][j] || dp[i][j+1];
}
}
}
return dp[0][0];
}
}
}6、购买足量干草的最小花费
题目描述: 有n个提供干草的公司,每个公司都有两个信息 cost[i]代表购买1次产品需要花的钱 val[i]代表购买1次产品所获得的干草数量 每个公司的产品都可以购买任意次 你一定要至少购买h数量的干草,返回最少要花多少钱
解题思路:
本题实质还是一个完全背包问题,
但是本题有一个难点在于至少购买h数量的干草,而每个公司购买一次的到的干草数不同,是很难购买后恰好有h的干草
所以这个里要花费最少的钱买到至少h的干草,我们以往定义的dp[i] [j] : 1... i里挑公司,购买严格j磅干草,需要的最少花费这种,就需要在最后有一定的转换
因为无法确定花最少的钱的到的干草数量恰好为h,因此花费最少的钱的到的干草量可能是大于h的,那么最小值就不一定在dp[n] [h]上,
但是我们也不能无限制的查找h后面的量(如果无限制那么给定的dp数组就无限大,没法做)
如果我们只买一种商品得到干草为w,需要至少h的量,那么这个商品最后拿到的干草量一定是w的整数倍,离h最近的一定在h, h+w的范围内
由此, 多个公司买干草,最后的范围一定在h+max_w中。即代码中的h+maxP。
最后做这个题,还有两个自身经常犯的问题,一是完全背包的空间压缩循环顺序经常写成01背包的,二是dp数组的初始化数值搞错
代码:
package main.java.class074;
import java.io.*;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code06_BuyingHayMinimumCost
* @description: 购买足量干草的最小花费
* // 有n个提供干草的公司,每个公司都有两个信息
* // cost[i]代表购买1次产品需要花的钱
* // val[i]代表购买1次产品所获得的干草数量
* // 每个公司的产品都可以购买任意次
* // 你一定要至少购买h数量的干草,返回最少要花多少钱
* // 测试链接 : https://www.luogu.com.cn/problem/P2918
* @author: zs宝
* @create: 2025-09-06 15:19
* @Version 1.0
**/public class Code06_BuyingHayMinimumCost {
public static int MAXN=101;
public static int MAXH=55001;
public static int n,h;
public static int[]cost=new int[MAXN];
public static int[]val=new int[MAXN];
public static int maxP;
public static int[]dp=new int[MAXH];
public static void main(String[] args) throws IOException {
BufferedReader buffer=new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in=new StreamTokenizer(buffer);
PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken()!=StreamTokenizer.TT_EOF){
n=(int)in.nval;
in.nextToken();
h=(int) in.nval;
maxP=-1;
for(int i=1;i<=n;i++){
in.nextToken();
val[i]=(int) in.nval;
//找出所有公司买一次的干草重量最大值
maxP=Math.max(maxP,val[i]);
in.nextToken();
cost[i]=(int) in.nval;
}
out.println(compute1());
}
out.flush();
out.close();
buffer.close();
}
//严格依赖位置的动态规划
// dp[i][j] : 1...i里挑公司,购买严格j磅干草,需要的最少花费
// 1) dp[i-1][j]
// 2) dp[i][j-val[i]] + cost[i] // 两种可能性中选最小
public static int compute1(){
int[][]dp=new int[n+1][h+maxP+1];
//Arrays.fill(dp[0], 1, h+maxP + 1, Integer.MAX_VALUE);
for(int i=0;i<=n;i++){
Arrays.fill(dp[i],Integer.MAX_VALUE);
}
dp[0][0] = 0;
for(int i=1;i<=n;i++){
for(int j=0;j<=h+maxP;j++){
dp[i][j]=dp[i-1][j];
if(j-val[i]>=0 && dp[i][j - val[i]] != Integer.MAX_VALUE){
dp[i][j]=Math.min(dp[i][j],dp[i][j-val[i]]+cost[i]);
}
}
}
int ans=Integer.MAX_VALUE;
for(int j=h;j<=h+maxP;j++){
ans=Math.min(ans,dp[n][j]);
}
return ans;
}
//严格依赖位置的动态规划+空间压缩
public static int compute2(){
Arrays.fill(dp,1,h+maxP+1,Integer.MAX_VALUE);
for(int i=1;i<=n;i++){
for(int j=val[i];j<=h+maxP;j++){
if(dp[j - val[i]] != Integer.MAX_VALUE){
dp[j]=Math.min(dp[j],dp[j-val[i]]+cost[i]);
}
}
}
int ans=Integer.MAX_VALUE;
for(int j=h;j<=h+maxP;j++){
ans=Math.min(ans,dp[j]);
}
return ans;
}
}