核心思想

区间dp：大范围的问题拆分成若干小范围的问题来求解

可能性展开的常见方式：

1）基于两侧端点讨论的可能性展开（1,2题）

2）基于范围上划分点的可能性展开（3,4,5,6题）

例题

1、让字符串成为回文串的最少插入次数

题目描述： 给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。

请你返回让 s 成为回文串的 最少操作次数 。

「回文串」是正读和反读都相同的字符串。

示例 1：

输入：s = "zzazz" 输出：0 解释：字符串 "zzazz" 已经是回文串了，所以不需要做任何插入操作。

示例 2：

输入：s = "mbadm" 输出：2 解释：字符串可变为 "mbdadbm" 或者 "mdbabdm" 。

示例 3：

输入：s = "leetcode" 输出：5 解释：插入 5 个字符后字符串变为 "leetcodocteel" 。

提示：

  • 1 <= s.length <= 500

  • s 中所有字符都是小写字母。

解题思路：

  • 区间dp基于两侧端点讨论的可能性展开

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 1312 + 让字符串成为回文串的最少插入次数

🧠 题目关键词（原文关键词）

字符串，插入变成回文串，最少操作次数

🧩 抽象问题类型（题目本质）

回文串

🔍 数据规模 / 限制

- 1 <= s.length <= 500 - s 中所有字符都是小写字母

🧭 我的初步思路

暴力递归

✅ 正确解法类型

区间dp

❗ 没想到的原因

想到了

📦 归入的题型分类

区间dp

🧠 触发词（以后遇到就联想）

将字符串变为回文串的最少操作次数->区间dp

🧪 解法一句话总结

当字符串长度大于2时，从两边向中间靠，每次判断左右边界字符是否相等，不等则插入新的字符，这个字符可以匹配左边界的，也可以匹配右边界的

代码如下

 package main.java.class076;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code01_MinimumInsertionToPalindrome  
  * @description: 让字符串成为回文串的最少插入次数  
  * // 给你一个字符串 s  
  * // 每一次操作你都可以在字符串的任意位置插入任意字符  
  * // 请你返回让s成为回文串的最少操作次数  
  * // 测试链接 : https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/  
  * @author: zs宝  
  * @create: 2025-09-12 14:33  
  * @Version 1.0  
  **/public class Code01_MinimumInsertionToPalindrome {  
     class Solution {  
         public int minInsertions(String s) {  
             return minInsertions4(s);  
         }  
   
         /**  
          暴力递归  
          */  
         public int minInsertions1(String str) {  
             char[] s = str.toCharArray();  
             int n = s.length;  
             return f1(s, 0, n - 1);  
         }  
   
         //s[i,j]范围内最少要插入几次可以使s[i,j]变为回文子串  
         public int f1(char[] s, int l, int r) {  
             //如果只有一个字符  
             if (l == r) {  
                 return 0;  
             }  
             //如果有两个  
             if (l + 1 == r) {  
                 return s[l] == s[r] ? 0 : 1;  
             }  
             //如果有多个  
             if (s[l] == s[r]) {  
                 return f1(s, l + 1, r - 1);  
             } else {  
                 //不同，则需要插入1次，那么有可能插入是为了和s[l]配对，也有可能插入是为了与s[r]配对  
                 return Math.min(f1(s, l, r - 1), f1(s, l + 1, r)) + 1;  
             }  
         }  
   
         /**  
          记忆化搜索：由暴力递归优化而来  
          */  
         public int minInsertions2(String str) {  
             char[] s = str.toCharArray();  
             int n = s.length;  
             int[][] dp = new int[n][n];  
             for (int i = 0; i < n; i++) {  
                 for (int j = i; j < n; j++) {  
                     dp[i][j] = -1;  
                 }  
             }  
             return f2(s, 0, n - 1, dp);  
         }  
   
         //s[i,j]范围内最少要插入几次可以使s[i,j]变为回文子串  
         public int f2(char[] s, int l, int r, int[][] dp) {  
             if (dp[l][r] != -1) {  
                 return dp[l][r];  
             }  
             int ans;  
             //如果只有一个字符  
             if (l == r) {  
                 ans = 0;  
             } else if (l + 1 == r) {  
                 //如果有两个  
                 ans = s[l] == s[r] ? 0 : 1;  
             } else {  
                 //如果有多个  
                 if (s[l] == s[r]) {  
                     ans = f2(s, l + 1, r - 1, dp);  
                 } else {  
                     //不同，则需要插入1次，那么有可能插入是为了和s[l]配对，也有可能插入是为了与s[r]配对  
                     ans = Math.min(f2(s, l, r - 1, dp), f2(s, l + 1, r, dp)) + 1;  
                 }  
             }  
             dp[l][r] = ans;  
             return ans;  
         }  
   
         /**  
          严格按照位置依赖的动态规划：有记忆化搜索优化而来  
          */  
         public int minInsertions3(String str) {  
             char[] s = str.toCharArray();  
             int n = s.length;  
             int[][] dp = new int[n][n];  
             for(int i=0;i<n-1;i++){  
                 dp[i][i+1]=s[i]==s[i+1]?0:1;  
             }  
             for(int i=n-3;i>=0;i--){  
                 for(int j=i+2;j<n;j++){  
                     if(s[i]==s[j]){  
                         dp[i][j]=dp[i+1][j-1];  
                     }else{  
                         dp[i][j]=Math.min(dp[i][j-1],dp[i+1][j])+1;  
                     }  
                 }  
             }  
             return dp[0][n-1];  
         }  
   
         /**  
          严格按照位置依赖的动态规划+空间压缩  
          */  
         public int minInsertions4(String str) {  
             char[] s = str.toCharArray();  
             int n = s.length;  
             if(n<2){  
                 return 0;  
             }  
             int[]dp = new int[n];  
             //第n-2行初始化  
             dp[n-1]=s[n-1]==s[n-2]?0:1;  
             for(int l=n-3,leftDown,backDown;l>=0;l--){  
                 leftDown=dp[l+1];  
                 dp[l+1]=s[l]==s[l+1]?0:1;  
                 for(int r=l+2;r<n;r++){  
                     backDown=dp[r];  
                     if(s[l]==s[r]){  
                         dp[r]=leftDown;  
                     }else{  
                         dp[r]=Math.min(dp[r-1],backDown)+1;  
                     }  
                     leftDown=backDown;  
                 }  
             }  
             return dp[n-1];  
         }  
   
     }  
 }

2、预测赢家

题目描述： 给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。

玩家 1 和玩家 2 轮流进行自己的回合，玩家 1 先手。开始时，两个玩家的初始分值都是 0 。每一回合，玩家从数组的任意一端取一个数字（即，nums[0] 或 nums[nums.length - 1]），取到的数字将会从数组中移除（数组长度减 1 ）。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时，游戏结束。

如果玩家 1 能成为赢家，返回 true 。如果两个玩家得分相等，同样认为玩家 1 是游戏的赢家，也返回 true 。你可以假设每个玩家的玩法都会使他的分数最大化。

示例 1：

输入：nums = [1,5,2] 输出：false 解释：一开始，玩家 1 可以从 1 和 2 中进行选择。 如果他选择 2（或者 1 ），那么玩家 2 可以从 1（或者 2 ）和 5 中进行选择。如果玩家 2 选择了 5 ，那么玩家 1 则只剩下 1（或者 2 ）可选。 所以，玩家 1 的最终分数为 1 + 2 = 3，而玩家 2 为 5 。 因此，玩家 1 永远不会成为赢家，返回 false 。

示例 2：

输入：nums = [1,5,233,7] 输出：true 解释：玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个，玩家 1 都可以选择 233 。 最终，玩家 1（234 分）比玩家 2（12 分）获得更多的分数，所以返回 true，表示玩家 1 可以成为赢家。

提示：

  • 1 <= nums.length <= 20

  • 0 <= nums[i] <= 107

解题思路：

  • 区间dp基于两侧端点讨论的可能性展开

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 486 + 预测赢家

🧠 题目关键词（原文关键词）

每轮选手只能选边界的一个数字

🧩 抽象问题类型（题目本质）

区间dp

🔍 数据规模 / 限制

- 1 <= nums.length <= 20 - 0 <= nums[i] <= 107

🧭 我的初步思路

区间dp

✅ 正确解法类型

区间dp

❗ 没想到的原因

在考虑范围内的数字长度大于3个时，想到了当前选手选当前数字会分类讨论，但是没有想明白，另外的选手选后，当前选手的下一轮该如何表示

📦 归入的题型分类

区间dp

🧠 触发词（以后遇到就联想）

数组从两边往中间选则的找最大赢家问题->区间dp

🧪 解法一句话总结

区间dp标准解法，基于两侧端点讨论的可能性展开

代码如下：

 package main.java.class076;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code02_PredictTheWinner  
  * @description: 预测赢家  
  * // 给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏  
  * // 玩家 1 和玩家 2 轮流进行自己的回合，玩家 1 先手  
  * // 开始时，两个玩家的初始分值都是 0  
  * // 每一回合，玩家从数组的任意一端取一个数字  
  * // 取到的数字将会从数组中移除，数组长度减1  
  * // 玩家选中的数字将会加到他的得分上  
  * // 当数组中没有剩余数字可取时游戏结束  
  * // 如果玩家 1 能成为赢家，返回 true  
  * // 如果两个玩家得分相等，同样认为玩家 1 是游戏的赢家，也返回 true  
  * // 你可以假设每个玩家的玩法都会使他的分数最大化  
  * // 测试链接 : https://leetcode.cn/problems/predict-the-winner/  
  * @author: zs宝  
  * @create: 2025-09-12 15:30  
  * @Version 1.0  
  **/public class Code02_PredictTheWinner {  
     class Solution {  
   
         public boolean predictTheWinner(int[] nums) {  
             return predictTheWinner3(nums);  
         }  
   
         public boolean predictTheWinner1(int[] nums) {  
             int n=nums.length;  
             int sum=0;  
             for(int i=0;i<n;i++){  
                 sum+=nums[i];  
             }  
             int firstSum=f1(nums,0,n-1);  
             int secondSum=sum-firstSum;  
             return firstSum>=secondSum;  
         }  
   
         /**  
          从i，j的范围内选择  
          */  
         public int f1(int[]nums,int l,int r){  
             if(l==r){  
                 return nums[l];  
             }else if(l+1==r){  
                 return Math.max(nums[l],nums[r]);  
             }else{  
                 //不止一个数  
                 //分类讨论当前拿边界的那个数，但是为了赢，另外一个人一定会让当前这个人个人拿到剩余的较小的数  
                 int ans1=nums[l]+Math.min(f1(nums,l+2,r),f1(nums,l+1,r-1));  
                 int ans2=nums[r]+Math.min(f1(nums,l+1,r-1),f1(nums,l,r-2));  
                 return Math.max(ans1,ans2);  
             }  
         }  
   
         //记忆化搜索  
         public boolean predictTheWinner2(int[] nums) {  
             int n=nums.length;  
             int sum=0;  
             for(int i=0;i<n;i++){  
                 sum+=nums[i];  
             }  
             int[][]dp=new int[n][n];  
             int firstSum=f2(nums,0,n-1,dp);  
             int secondSum=sum-firstSum;  
             return firstSum>=secondSum;  
         }  
   
         /**  
          从i，j的范围内选择  
          */  
         public int f2(int[]nums,int l,int r,int[][]dp){  
             if(dp[l][r]!=0){  
                 return dp[l][r];  
             }  
             int ans;  
             if(l==r){  
                 ans= nums[l];  
             }else if(l+1==r){  
                 ans= Math.max(nums[l],nums[r]);  
             }else{  
                 //不止一个数  
                 //分类讨论当前拿边界的那个数，但是为了赢，另外一个人一定会让当前这个人个人拿到剩余的较小的数  
                 int ans1=nums[l]+Math.min(f2(nums,l+2,r,dp),f2(nums,l+1,r-1,dp));  
                 int ans2=nums[r]+Math.min(f2(nums,l+1,r-1,dp),f2(nums,l,r-2,dp));  
                 ans= Math.max(ans1,ans2);  
             }  
             dp[l][r]=ans;  
             return ans;  
         }  
   
   
         //严格按照位置依赖的动态规划  
         public boolean predictTheWinner3(int[] nums) {  
             int n=nums.length;  
             int sum=0;  
             for(int i=0;i<n;i++){  
                 sum+=nums[i];  
             }  
             int[][]dp=new int[n][n];  
             dp[n-1][n-1]=nums[n-1];  
             for(int i=0;i<n-1;i++){  
                 dp[i][i]=nums[i];  
                 dp[i][i+1]=Math.max(nums[i],nums[i+1]);  
             }  
             for(int l=n-3;l>=0;l--){  
                 for(int r=l+2,ans1,ans2;r<n;r++){  
                     ans1=nums[l]+Math.min(dp[l+2][r],dp[l+1][r-1]);  
                     ans2=nums[r]+Math.min(dp[l+1][r-1],dp[l][r-2]);  
                     dp[l][r]=Math.max(ans1,ans2);  
                 }  
             }  
             int firstSum=dp[0][n-1];  
             int secondSum=sum-firstSum;  
             return firstSum>=secondSum;  
         }  
     }  
 }

3、多边形三角剖分的最低得分

题目描述： 你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

示例 1：

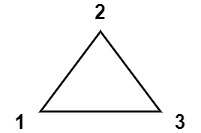
输入：values = [1,2,3] 输出：6 解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

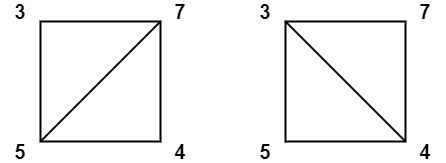
输入：values = [3,7,4,5] 输出：144 解释：有两种三角剖分，可能得分分别为：375 + 457 = 245，或 345 + 347 = 144。最低分数为 144。

示例 3：

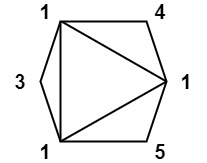
输入：values = [1,3,1,4,1,5] 输出：13 解释：最低分数三角剖分的得分情况为 113 + 114 + 115 + 111 = 13。

提示：

  • n == values.length

  • 3 <= n <= 50

  • 1 <= values[i] <= 100

解题思路

  • 区间dp，基于范围上划分点的可能性展开

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 1039 + 多边形三角剖分的最低得分

🧠 题目关键词（原文关键词）

多边形剖三角形，最低得分

🧩 抽象问题类型（题目本质）

区间dp

🔍 数据规模 / 限制

- n == values.length - 3 <= n <= 50 - 1 <= values[i] <= 100

🧭 我的初步思路

区间dp

✅ 正确解法类型

区间dp

❗ 没想到的原因

识别出来了，但是写的递归却错了，我想的是[l, r]间有三个数值时作为一个三角形的乘积，对于三个，则选择任一点将其分开为两半，进行求解。但实际应该从中任选一点与边界点围城三角形+从边界点切开的两边将会得到的三角形累和

📦 归入的题型分类

区间dp

🧠 触发词（以后遇到就联想）

多边形多边形剖三角形，最低得分->区间dp

🧪 解法一句话总结

基于范围上划分点的可能性展开

代码如下

 package main.java.class076;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code03_MinimumScoreTriangulationOfPolygon  
  * @description: 多边形三角剖分的最低得分  
  * // 你有一个凸的 n 边形，其每个顶点都有一个整数值  
  * // 给定一个整数数组values，其中values[i]是第i个顶点的值(顺时针顺序)  
  * // 假设将多边形 剖分 为 n - 2 个三角形  
  * // 对于每个三角形，该三角形的值是顶点标记的乘积  
  * // 三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和  
  * // 返回 多边形进行三角剖分后可以得到的最低分  
  * // 测试链接 : https://leetcode.cn/problems/minimum-score-triangulation-of-polygon/  
  * @author: zs宝  
  * @create: 2025-09-12 16:11  
  * @Version 1.0  
  **/public class Code03_MinimumScoreTriangulationOfPolygon {  
     class Solution {  
         public int minScoreTriangulation(int[] values) {  
             return  minScoreTriangulation2(values);  
         }  
   
         //记忆化搜索  
         public int minScoreTriangulation1(int[] values) {  
             int n=values.length;  
             int[][]dp=new int[n][n];  
             for(int i=0;i<n;i++){  
                 for(int j=0;j<n;j++){  
                     dp[i][j]=-1;  
                 }  
             }  
             return  f1(values,0,n-1,dp);  
         }  
   
         //dp[i][j]:表示[i,j]点划分出的三角形中累和的最低得分  
         //如何构成三角形：从(i,j)之间选择一个点出来与i，j构成三角形，然后分别再看(i,m),(m,j)构成的三角形中累和  
         public int f1(int[] values,int l,int r,int[][]dp){  
             if(dp[l][r]!=-1){  
                 return dp[l][r];  
             }  
             int ans=Integer.MAX_VALUE;  
             //只有1个或者2个数字  
             if(l==r || l+1==r){  
                 ans=0;  
             }else{  
                 for(int m=l+1;m<r;m++){  
                     ans=Math.min(ans,f1(values,l,m,dp)+f1(values,m,r,dp)+values[l]*values[m]*values[r]);  
                 }  
             }  
             dp[l][r]=ans;  
             return ans;  
         }  
   
         //严格按照位置依赖的动态规划  
         public int minScoreTriangulation2(int[] values) {  
             int n=values.length;  
             int[][]dp=new int[n][n];  
             for(int l=n-3;l>=0;l--){  
                 for(int r=l+2;r<n;r++){  
                     dp[l][r]=Integer.MAX_VALUE;  
                     for(int m=l+1;m<r;m++){  
                         dp[l][r]=Math.min(dp[l][r],dp[l][m]+dp[m][r]+values[l]*values[m]*values[r]);  
                     }  
                 }  
             }  
             return  dp[0][n-1];  
         }  
     }  
 }

4、切棍子的最小成本

题目描述： 有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

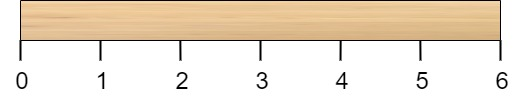
给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

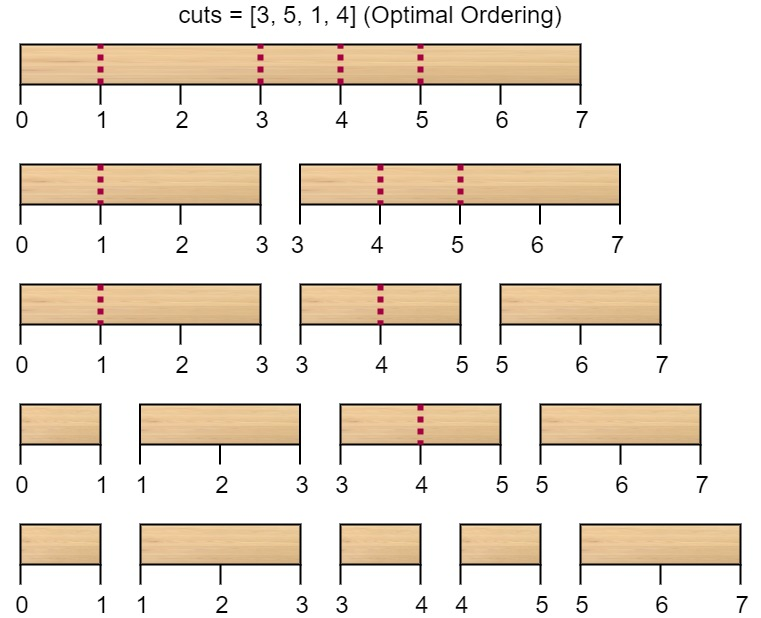
输入：n = 7, cuts = [1,3,4,5] 输出：16 解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示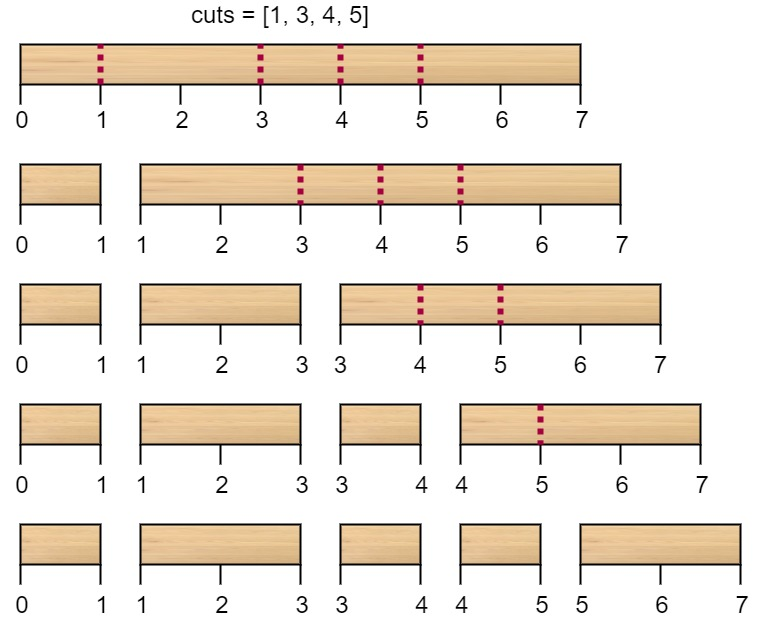： 第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。 而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2] 输出：22 解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：

  • 2 <= n <= 10^6

  • 1 <= cuts.length <= min(n - 1, 100)

  • 1 <= cuts[i] <= n - 1

  • cuts 数组中的所有整数都 互不相同

项目名称

内容填写

📘 题目编号 / 标题

LeetCode 1547. Minimum Cost to Cut a Stick（最小切割成本）

🧠 题目关键词（原文关键词）

切割顺序、总成本、区间、最小化、动态规划、interval DP、partition

🧩 抽象问题类型（题目本质）

区间 DP（按位置划分点），与“矩阵链乘/石子合并/戳气球”同类：在区间上选择一个切点将问题分成左右两段，代价与区间长度有关

🔍 数据规模 / 限制

cuts.length ≤ 100，n ≤ 1e6（仅作为端点），三重循环 O(m³) 可过（m = cuts.length）

🧭 我的初步思路

以为贪心按“最靠中间”或“长度最小的段”切，但很快发现局部最优不保证全局最优，需要全局搜索或 DP

✅ 正确解法类型

区间 DP：在排好序的切点数组（含两端哨兵 0 与 n）上做 DP；dp[l][r] 表示切掉 (l..r) 之间所有点的最小成本

❗ 没想到的原因

没给 cuts 排序，或没有加哨兵导致长度计算错；没有意识到“切某点的代价=当前整段长度=arr[r+1]-arr[l-1]”，从而无法写出区间状态

📦 归入的题型分类

[x] 区间 DP / 按划分点转移 [x] 矩阵链乘型 [x] 合并代价型

🧠 触发词（以后遇到就联想）

“切割/合并顺序影响总代价” + “每次代价=当前整段长度/权重” + “把一段分成两段/合并成一段” ⇒ 区间 DP

🧪 解法一句话总结

设 arr = [0, cuts..., n] 升序；dp[l][r] = min_{k∈[l..r]}( dp[l][k-1] + dp[k+1][r] ) + (arr[r+1]-arr[l-1])，答案 dp[1][m]（m=cuts数）。

代码如下：

 package main.java.class076;  
   
 import java.util.Arrays;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code04_MinimumCostToCutAStick  
  * @description: 切棍子的最小成本  
  * // 有一根长度为n个单位的木棍，棍上从0到n标记了若干位置  
  * // 给你一个整数数组cuts，其中cuts[i]表示你需要将棍子切开的位置  
  * // 你可以按顺序完成切割，也可以根据需要更改切割的顺序  
  * // 每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和  
  * // 对棍子进行切割将会把一根木棍分成两根较小的木棍  
  * // 这两根木棍的长度和就是切割前木棍的长度  
  * // 返回切棍子的最小总成本  
  * // 测试链接 : https://leetcode.cn/problems/minimum-cost-to-cut-a-stick/  
  * @author: zs宝  
  * @create: 2025-09-12 16:46  
  * @Version 1.0  
  **/public class Code04_MinimumCostToCutAStick {  
     class Solution {  
         public int minCost(int n, int[] cuts) {  
             return minCost2(n,cuts);  
         }  
   
         //记忆化搜索  
         public int minCost1(int n, int[] cuts) {  
             Arrays.sort(cuts);  
             int m=cuts.length;  
             int[]arr=new int[m+2];  
             arr[0]=0;  
             arr[m+1]=n;  
             for(int i=1;i<=m;i++){  
                 arr[i]=cuts[i-1];  
             }  
   
             int[][]dp=new int[m+2][m+2];  
             for(int i=0;i<m+2;i++){  
                 for(int j=0;j<m+2;j++){  
                     dp[i][j]=-1;  
                 }  
             }  
             return f1(arr,1,m,dp);  
         }  
   
         //这到题的难点在于，如何知道每次切的时候代价为多少  
         //代价=arr[r+1]-arr[l-1]  
         public int f1(int[] arr,int l,int r,int[][]dp){  
             if(l>r){  
                 return 0;  
             }  
             if(l==r){  
                 return arr[r+1]-arr[l-1];  
             }  
             if(dp[l][r]!=-1){  
                 return dp[l][r];  
             }  
             //接下来就是区间dp:基于范围上划分点的可能性展开  
             int ans=Integer.MAX_VALUE;  
             //由于[l,r]的点都可以被切  
             for(int m=l;m<=r;m++){  
                 ans=Math.min(f1(arr,l,m-1,dp)+f1(arr,m+1,r,dp),ans);  
             }  
             ans+=arr[r+1]-arr[l-1];  
             dp[l][r]=ans;  
             return ans;  
         }  
   
         //严格按照位置依赖的动态规划  
         public int minCost2(int n, int[] cuts) {  
             Arrays.sort(cuts);  
             int m=cuts.length;  
             int[]arr=new int[m+2];  
             arr[0]=0;  
             arr[m+1]=n;  
             for(int i=1;i<=m;i++){  
                 arr[i]=cuts[i-1];  
             }  
   
             int[][]dp=new int[m+2][m+2];  
             for(int i=1;i<=m;i++){  
                 dp[i][i]=arr[i+1]-arr[i-1];  
             }  
             for(int l=m-1;l>=1;l--){  
                 for(int r=l+1;r<=m;r++){  
                     dp[l][r]=Integer.MAX_VALUE;  
                     for(int k=l;k<=r;k++){  
                         dp[l][r]=Math.min(dp[l][k-1]+dp[k+1][r],dp[l][r]);  
                     }  
                     dp[l][r]+=arr[r+1]-arr[l-1];  
                 }  
             }  
             return dp[1][m];  
         }  
     }  
 }

5、戳气球

题目描述： 有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。

求所能获得硬币的最大数量。

示例 1：

输入：nums = [3,1,5,8] 输出：167 解释： nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> [] coins = 315 + 358 + 138 + 181 = 167

示例 2：

输入：nums = [1,5] 输出：10

提示：

  • n == nums.length

  • 1 <= n <= 300

  • 0 <= nums[i] <= 100

解题思路：

  • 区间dp：基于范围上划分点的可能性展开

  • 以往的题的划分点都是这个点作为最开始的点，放在本题就是这个点作为最开始打爆的气球

  • 本题根据题意，我们这里选择的划分点是某个点作为最后点的可能，放在本题即选择的点作为最后打爆的气球（根本想不到，太妙了）

项目名称

内容填写

📘 题目编号 / 标题

LeetCode 312 - Burst Balloons（戳气球）

🧠 题目关键词（原文关键词）

interval DP、区间动态规划、last-one strategy、加哨兵、最大化收益

🧩 抽象问题类型（题目本质）

区间 DP（按“最后一个”划分）：在区间 l,r 选择一个位置 k 作为最后戳的气球，收益为两侧子问题最优解 + 邻接乘积

🔍 数据规模 / 限制

- n == nums.length - 1 <= n <= 300 - 0 <= nums[i] <= 100

🧭 我的初步思路

直觉想按局部高分先戳/贪心，但相邻乘积会动态变化，局部最优不等于全局最优；需区间划分

✅ 正确解法类型

区间 DP：在首尾各加哨兵 11，令 arr = [1] + nums + [1]；用 dp[l][r] 表示在开区间 (l-1, r+1) 内把 arr[l..r] 全戳掉的最大硬币数

❗ 没想到的原因

未想到“最后戳谁”能固定邻接，从而把乘积变成常数；或忘记加哨兵 1 导致边界处理复杂

📦 归入的题型分类

[x] 区间 DP / 按划分点转移 [x] 合并/分割顺序优化

🧠 触发词（以后遇到就联想）

“戳/合并顺序影响收益” + “收益依赖当前区间两端” + “加哨兵后端点固定” ⇒ 选区间内最后一个元素做划分的区间 DP

🧪 解法一句话总结

加哨兵 11，设 dp[l][r] = max_{k∈[l..r]} ( dp[l][k-1] + dp[k+1][r] + arr[l-1]*arr[k]*arr[r+1] )，答案 dp[1][n]。

代码如下：

 package main.java.class076;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code05_BurstBalloons  
  * @description: 戳气球  
  * // 有 n 个气球，编号为0到n-1，每个气球上都标有一个数字，这些数字存在数组nums中  
  * // 现在要求你戳破所有的气球。戳破第 i 个气球  
  * // 你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币  
  * // 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号  
  * // 如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球  
  * // 求所能获得硬币的最大数量  
  * // 测试链接 : https://leetcode.cn/problems/burst-balloons/  
  * @author: zs宝  
  * @create: 2025-09-12 19:44  
  * @Version 1.0  
  **/public class Code05_BurstBalloons {  
     class Solution {  
         public int maxCoins(int[] nums) {  
             return maxCoins2(nums);  
         }  
   
         //记忆化搜索  
         public int maxCoins1(int[] nums) {  
             int n = nums.length;  
             int[] arr = new int[n + 2];  
             for (int i = 1; i <= n; i++) {  
                 arr[i] = nums[i - 1];  
             }  
             arr[0] = 1;  
             arr[n + 1] = 1;  
             int[][] dp = new int[n + 2][n + 2];  
             for (int i = 0; i < n + 2; i++) {  
                 for (int j = 0; j < n + 2; j++) {  
                     dp[i][j] = -1;  
                 }  
             }  
             return f1(arr, 1, n, dp);  
         }  
   
         //每一次调用这个函数都必须保证l-1,r+1位置的气球一定没有打爆  
         public int f1(int[] arr, int l, int r, int[][] dp) {  
             if (dp[l][r] != -1) {  
                 return dp[l][r];  
             }  
             int ans = Integer.MIN_VALUE;  
             if (l == r) {  
                 ans = arr[l - 1] * arr[l] * arr[r + 1];  
             } else {  
                 //接下来开始区间dp：基于范围上划分点的可能性展开  
                 //这里以往的题的划分点都是这个点作为最开始的点，放在本题就是这个点作为最开始打爆的气球  
                 //但是本题根据题意，我们这里选择的划分点是某个点作为最后点的可能，放在本题即选择的点作为最后打爆的气球  
                 //首先讨论两个边界点l,r作为最后打爆的点，那个值更大  
                 ans = Math.max(  
                         f1(arr, l + 1, r, dp) + arr[l - 1] * arr[l] * arr[r + 1],  
                         f1(arr, l, r - 1, dp) + arr[l - 1] * arr[r] * arr[r + 1]);  
                 //接着讨论中间的点  
                 for (int k = l + 1; k < r; k++) {  
                     ans = Math.max(ans, f1(arr, l, k - 1, dp) + f1(arr, k + 1, r, dp) + arr[l - 1] * arr[k] * arr[r + 1]);  
                 }  
             }  
             dp[l][r] = ans;  
             return ans;  
         }  
   
         //严格按照位置依赖的动态规划  
         public int maxCoins2(int[] nums) {  
             int n = nums.length;  
             int[] arr = new int[n + 2];  
             for (int i = 1; i <= n; i++) {  
                 arr[i] = nums[i - 1];  
             }  
             arr[0] = 1;  
             arr[n + 1] = 1;  
             int[][] dp = new int[n + 2][n + 2];  
             for (int i = 1; i <= n; i++) {  
                 dp[i][i] = arr[i - 1] * arr[i] * arr[i + 1];  
             }  
             for (int l = n - 1; l >= 1; l--) {  
                 for (int r = l + 1; r <= n; r++) {  
                     dp[l][r] = Math.max(  
                             dp[l + 1][r] + arr[l - 1] * arr[l] * arr[r + 1],  
                             dp[l][r - 1] + arr[l - 1] * arr[r] * arr[r + 1]);  
   
                     for (int k = l + 1; k < r; k++) {  
                         dp[l][r]=Math.max(dp[l][r], dp[l][k-1] + dp[k+1][r] + arr[l - 1] * arr[k] * arr[r + 1]);  
                     }  
                 }  
             }  
             return dp[1][n];  
         }  
   
     }  
 }

6、布尔运算

题目描述： 给定一个布尔表达式和一个期望的布尔结果 result，布尔表达式由 0 (false)、1 (true)、& (AND)、 | (OR) 和 ^ (XOR) 符号组成。实现一个函数，算出有几种可使该表达式得出 result 值的括号方法。

示例 1：

输入：s = "1^0|0|1", result = 0

输出：2 解释：两种可能的括号方法是 1^(0|(0|1)) 1^((0|0)|1)

示例 2：

输入：s = "0&0&0&1^1|0", result = 1

输出：10

提示：

  • 运算符的数量不超过 19 个

项目名称

内容填写

📘 题目编号 / 标题

LeetCode 面试题 08.14 /

🧠 题目关键词（原文关键词）

布尔表达式由 0 (false)、1 (true)、& (AND)、 \| (OR) 和 ^ (XOR) 符号组成

🧩 抽象问题类型（题目本质）

区间 DP（按运算符划分） + 计数型 DP（同时维护为 0/1 的方案数）

🔍 数据规模 / 限制

运算符数量 ≤ 19（表达式长度 ≤ 39）；O(n³) 可过

🧭 我的初步思路

递归枚举每个运算符作为最后计算点，将表达式拆左右子表达式，再按真/假的组合累加

✅ 正确解法类型

1) 记忆化搜索：f(i,j) 返回 [falseWays, trueWays]；2) 自底向上区间 DP：dp[i][j][2]

❗ 没想到的原因

忘了“数字和运算符交替、下标奇偶性”，导致状态越界；或只统计 true 没同时维护 false；或没有为每个 [i,j] 重新清零累加器

📦 归入的题型分类

[x] 区间 DP [x] 计数 DP [x] 表达式求值类

🧠 触发词（以后遇到就联想）

“表达式 + 加括号/求个数/最大值” + “按运算符分治/最后计算谁” ⇒ 区间 DP

🧪 解法一句话总结

令 dp[i][j][0/1] 表示 s[i..j] 为假/真的方案数；枚举运算符 k，按 `&

这个题的代码在最开始想的dp怎么做想到了，但是在写的过程中出现以下问题

  • 不知道每一个范围【i, j】的t, f的个数在取其中不同的运算符为最后一个运算符时该怎么算出，这么多的运算符可以为最后一个，老想着求最大最小，但就是忽略了题意求的是总量

  • 严格按照位置依赖的动态规划，在对每一个i, j的dp计算时，变量t, f的初始化位置没写对，导致每一个j的时候t, f都有值，一直累加

代码如下

 package main.java.class076;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code06_BooleanEvaluation  
  * @description: 布尔运算  
  * // 给定一个布尔表达式和一个期望的布尔结果 result  
  * // 布尔表达式由 0 (false)、1 (true)、& (AND)、 | (OR) 和 ^ (XOR) 符号组成  
  * // 布尔表达式一定是正确的，不需要检查有效性  
  * // 但是其中没有任何括号来表示优先级  
  * // 你可以随意添加括号来改变逻辑优先级  
  * // 目的是让表达式能够最终得出result的结果  
  * // 返回最终得出result有多少种不同的逻辑计算顺序  
  * // 测试链接 : https://leetcode.cn/problems/boolean-evaluation-lcci/  
  * @author: zs宝  
  * @create: 2025-09-12 20:38  
  * @Version 1.0  
  **/public class Code06_BooleanEvaluation {  
     class Solution {  
         public int countEval(String str, int result) {  
             return countEval2(str, result);  
         }  
   
         //记忆化搜索  
         public int countEval1(String str, int result) {  
             char[] s = str.toCharArray();  
             int n = s.length;  
             int[][][] dp = new int[n][n][];  
             int[] res = f1(s, 0, n - 1, dp);  
             return res[result];  
         }  
   
         //要保持i,j位置都是数字  
         //逻辑符号与数字交替  
         public int[] f1(char[] s, int i, int j, int[][][] dp) {  
             if (dp[i][j] != null) {  
                 return dp[i][j];  
             }  
             //在s[i,j]的范围内，求出false，true的表达式有多少种  
             int f = 0;  
             int t = 0;  
             if (i == j) {  
                 f = s[i] == '0' ? 1 : 0;  
                 t = s[i] == '1' ? 1 : 0;  
             } else {  
                 //选择那个运算符，最后计算  
                 //对于当前表达式，最终true，false的个数对于每一个运算符结尾的可能累加即可  
                 int[] temp;  
                 for (int k = i + 1, a, b, c, d; k < j; k += 2) {  
                     //temp，0位置存储false的数量，1位置存储true的数量  
                     temp = f1(s, i, k - 1, dp);  
                     a = temp[0];  
                     b = temp[1];  
                     temp = f1(s, k + 1, j, dp);  
                     c = temp[0];  
                     d = temp[1];  
                     if (s[k] == '&') {  
                         f += a * c + a * d + b * c;  
                         t += b * d;  
                     } else if (s[k] == '|') {  
                         f += a * c;  
                         t += b * d + a * d + b * c;  
                     } else {  
                         f += a * c + b * d;  
                         t += a * d + b * c;  
                     }  
                 }  
             }  
             int[] ans = new int[] { f, t };  
             dp[i][j] = ans;  
             return ans;  
         }  
   
         //严格依赖位置的动态规划  
         public int countEval2(String str, int result) {  
             char[] s = str.toCharArray();  
             int n = s.length;  
             int[][][] dp = new int[n][n][2];  
             for (int i = 0; i < n; i++) {  
                 dp[i][i][0] = s[i] == '0' ? 1 : 0;  
                 dp[i][i][1] = s[i] == '1' ? 1 : 0;  
             }  
             for (int i = n - 3; i >= 0; i-=2) {  
                 for (int j = i + 2; j < n; j += 2) {  
                     int f=0;  
                     int t=0;  
                     for (int k = i + 1, a, b, c, d; k < j; k += 2) {  
                         a = dp[i][k - 1][0];  
                         b = dp[i][k - 1][1];  
                         c = dp[k + 1][j][0];  
                         d = dp[k + 1][j][1];  
                         if (s[k] == '&') {  
                             f += a * c + a * d + b * c;  
                             t += b * d;  
                         } else if (s[k] == '|') {  
                             f += a * c;  
                             t += b * d + a * d + b * c;  
                         } else {  
                             f += a * c + b * d;  
                             t += a * d + b * c;  
                         }  
                     }  
                     dp[i][j][0]=f;  
                     dp[i][j][1]=t;  
                 }  
             }  
             return dp[0][n - 1][result];  
         }  
     }  
 }

参考资料