核心思想
树
头节点没有父亲,其他节点只有一个父亲的有向无环图,直观理解为发散状 在树上,从头节点出发到任何节点的路径是唯一的,不管二叉树还是多叉树都如此
树型dp在树上做动态规划,依赖关系比一般动态规划简单, 因为绝大部分多数都是父依赖子 只是依赖关系简单,不代表题目简单
树型dp套路
1)分析父树得到答案需要子树的哪些信息
2)把子树信息的全集定义成递归返回值
3)通过递归让子树返回全集信息(一般的递归就是看要不要考虑当前节点)
4)整合子树的全集信息得到父树的全集信息并返回
例题
1、二叉搜索子树的最大键值和
题目描述: 给你一棵以 root 为根的 二叉树 ,请你返回 任意 二叉搜索子树的最大键值和。
二叉搜索树的定义如下:
任意节点的左子树中的键值都 小于 此节点的键值。
任意节点的右子树中的键值都 大于 此节点的键值。
任意节点的左子树和右子树都是二叉搜索树。
示例 1:
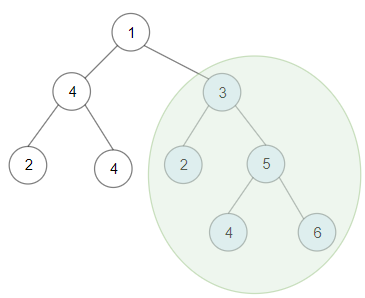
输入:root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6] 输出:20 解释:键值为 3 的子树是和最大的二叉搜索树。
示例 2:
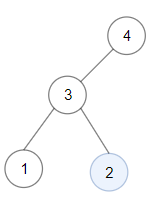
输入:root = [4,3,null,1,2] 输出:2 解释:键值为 2 的单节点子树是和最大的二叉搜索树。
示例 3:
输入:root = [-4,-2,-5] 输出:0 解释:所有节点键值都为负数,和最大的二叉搜索树为空。
示例 4:
输入:root = [2,1,3] 输出:6
示例 5:
输入:root = [5,4,8,3,null,6,3] 输出:7
提示:
每棵树有
1到40000个节点。每个节点的键值在
[-4 * 10^4 , 4 * 10^4]之间。
解题思路:
这个题我们就依据核心思想中的树型dp步骤来写
首先是分析父树得到答案需要子树的哪些信息
首先根据搜索二叉树的定义,左子树都要比当前节点小,右子树都要比当前节点大,那么父节点就需要子树节点的最大值
max,最小值min又因为本题是求二叉搜索子树的最大键值和,因此我们还需要一个变量用于表示当前子树是否为二叉搜索子树
isBST,以及子树的二叉搜索子树的最大键值和maxBstSum被我忽略的,最后如果一个子树如果是二叉搜索树,那么其二叉搜索子树的最大键值和就为这个子树所有节点的数值和,所以这里还需要一个
sum来辅助寻找最大键值和
然后将上述信息全集定义成递归返回值
设定递归的到整个树的信息
代码如下:
package main.java.class078;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code02_MaximumSumBst
* @description: 二叉搜索子树的最大键值和
* // 给你一棵以 root 为根的二叉树
* // 请你返回 任意 二叉搜索子树的最大键值和
* // 二叉搜索树的定义如下:
* // 任意节点的左子树中的键值都 小于 此节点的键值
* // 任意节点的右子树中的键值都 大于 此节点的键值
* // 任意节点的左子树和右子树都是二叉搜索树
* // 测试链接 : https://leetcode.cn/problems/maximum-sum-bst-in-binary-tree/
* @author: zs宝
* @create: 2025-09-19 09:07
* @Version 1.0
**/public class Code02_MaximumSumBst {
// 不要提交这个类
public static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
}
// 提交如下的方法
public static int maxSumBST(TreeNode root) {
return f(root).maxBstSum;
}
//分析父树得到答案寻妖那些信息
public static class info{
//树中最大值
int max;
//树中节点最小值
int min;
//所有节点和
int sum;
//是不是二叉搜索树
boolean isBST;
//二叉搜索树节点和
int maxBstSum;
public info(int a,int b,int c,boolean d,int e){
max=a;
min=b;
sum=c;
isBST=d;
maxBstSum=e;
}
}
public static info f(TreeNode node){
if(node==null){
return new info(Integer.MIN_VALUE,Integer.MAX_VALUE,0,true,0);
}
info left=f(node.left);
info right=f(node.right);
int max=Math.max(node.val,Math.max(left.max, right.max));
int min=Math.min(node.val,Math.min(left.min, right.min));
boolean isBST= left.isBST && right.isBST && left.max< node.val && right.min> node.val;
int sum= left.sum+node.val+right.sum;
int maxBstSum=Math.max(left.maxBstSum, right.maxBstSum);
if(isBST){
maxBstSum=Math.max(sum,maxBstSum);
}
return new info(max,min,sum,isBST,maxBstSum);
}
}2、二叉树的直径
题目描述: 给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:

输入:root = [1,2,3,4,5] 输出:3 解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2] 输出:1
提示:
树中节点数目在范围
[1, 104]内-100 <= Node.val <= 100
解题思路:
确认父树需要子树的那些信息:子树的直径,子树的高度
递归,直径需要经过当前节点,直径不需要经过当前节点
我的错误,在考虑以当前节点为根节点的数,若直径需要经过当前节点时,那么直径应该为左右子树的高度之和,而我算的是高度之和加一,这是没有好好区分树的高度值与本节计算直径(直径要的是边的个数)的区别
代码如下
package main.java.class078;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code03_DiameterOfBinaryTree
* @description: 二叉树的直径
* // 给你一棵二叉树的根节点,返回该树的直径
* // 二叉树的 直径 是指树中任意两个节点之间最长路径的长度
* // 这条路径可能经过也可能不经过根节点 root
* // 两节点之间路径的 长度 由它们之间边数表示
* // 测试链接 : https://leetcode.cn/problems/diameter-of-binary-tree/
* @author: zs宝
* @create: 2025-09-19 09:54
* @Version 1.0
**/public class Code03_DiameterOfBinaryTree {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public static int diameterOfBinaryTree(TreeNode root) {
return f(root).diameter;
}
public static class info{
int diameter;
int height;
public info(int a,int b){
diameter=a;
height=b;
}
}
public static info f(TreeNode x){
if(x==null){
return new info(0,0);
}
info left=f(x.left);
info right=f(x.right);
//若直径要经过当前节点。则直径为子树高度之和+1
int diameter=left.height+right.height;
//若不经过当前节点,则直径为左右子树的最大直径
diameter=Math.max(diameter,Math.max(left.diameter,right.diameter));
int height=Math.max(left.height,right.height)+1;
return new info(diameter,height);
}
}3、在二叉树中分配硬币
题目描述: 给你一个有 n 个结点的二叉树的根结点 root ,其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。
在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点,或者从子结点移动到父结点。
返回使每个结点上 只有 一枚硬币所需的 最少 移动次数。
示例 1:
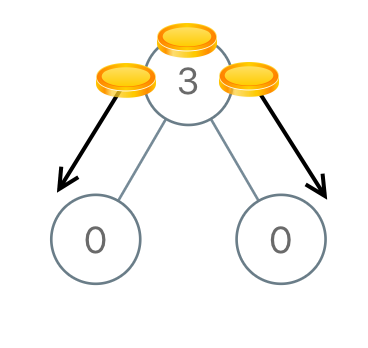
输入:root = [3,0,0] 输出:2 解释:一枚硬币从根结点移动到左子结点,一枚硬币从根结点移动到右子结点。
示例 2:
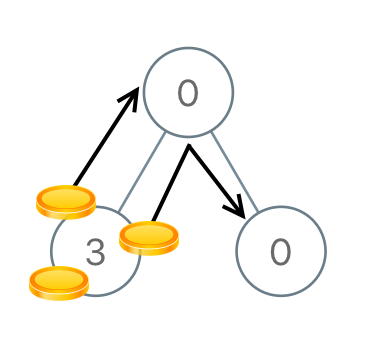
输入:root = [0,3,0] 输出:3 解释:将两枚硬币从根结点的左子结点移动到根结点(两次移动)。然后,将一枚硬币从根结点移动到右子结点。
提示:
树中节点的数目为
n1 <= n <= 1000 <= Node.val <= n所有
Node.val的值之和是n
解题思路:
树上每个结点想要 正好 1 枚硬币;
如果某个结点多了/少了,就需要通过边和父子交换;
问:最少多少次交换能把所有结点调成 1 枚。
每条边上的硬币移动次数,等于子树对外的“净盈余/净亏空”
如果某个子树一共 5 枚硬币,但里面有 3 个结点,那么它比理想的 3 枚多出 2 枚。 这 2 枚必须流出去,至少要经过边 2 次。
如果某个子树只有 1 枚硬币,但里面有 3 个结点,那么它缺 2 枚。 这 2 枚必须从外面流进来,也至少要经过边 2 次。
每个子树的盈余/亏空值 = 子树总硬币数 - 子树结点数。
代码如下
package main.java.class078;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code04_DistributeCoins
* @description: 在二叉树中分配硬币
* // 给你一个有 n 个结点的二叉树的根结点 root
* // 其中树中每个结点 node 都对应有 node.val 枚硬币
* // 整棵树上一共有 n 枚硬币
* // 在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点
* // 移动可以是从父结点到子结点,或者从子结点移动到父结点
* // 返回使每个结点上 只有 一枚硬币所需的 最少 移动次数
* // 测试链接 : https://leetcode.cn/problems/distribute-coins-in-binary-tree/
* @author: zs宝
* @create: 2025-09-19 10:38
* @Version 1.0
**/public class Code04_DistributeCoins {
public static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
}
public static int ans;
public int distributeCoins(TreeNode root) {
ans=0;
f(root);
return ans;
}
public static class info{
int coins;
int nodes;
public info(int a,int b){
coins=a;
nodes=b;
}
}
public static info f(TreeNode x){
if(x==null){
return new info(0,0);
}
info left=f(x.left);
info right=f(x.right);
int nodes=left.nodes+right.nodes+1;
int coins=x.val+left.coins+right.coins;
ans+=(Math.abs(left.coins-left.nodes)+Math.abs(right.coins-right.nodes));
return new info(coins,nodes);
}
}5、没有上司的舞会
题目描述 某大学有 n 个职员,编号为 1\ldots n。
他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。
现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 r_i,但是呢,如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。
所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。 输入格式
输入的第一行是一个整数 n。
第 2 到第 (n + 1) 行,每行一个整数,第 (i+1) 行的整数表示 i 号职员的快乐指数 r_i。
第 (n + 2) 到第 2n 行,每行输入一对整数 l, k,代表 k 是 l 的直接上司。 输出格式
输出一行一个整数代表最大的快乐指数。 输入输出样例 #1
输入 #1
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5输出 #1
5说明/提示 数据规模与约定
对于 100\% 的数据,保证 1\leq n \leq 6 \times 10^3,-128 \leq r_i\leq 127,1 \leq l, k \leq n,且给出的关系一定是一棵树。
这个题就是一个变形的打家劫舍问题,十分类似,都是讨论当前节点要不要,要的话下一个节点只能选择不要,当前节点不要的话,那么就像选下一个节点的要与不要的较大值
代码如下
package main.java.class078;
import java.io.*;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code05_Dancing
* @description: 没有上司的舞会
* // 某大学有n个职员,编号为1...n
* // 他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树
* // 父结点就是子结点的直接上司
* // 现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数
* // 但是如果某个职员的直接上司来参加舞会了
* // 那么这个职员就无论如何也不肯来参加舞会了
* // 所以请你编程计算邀请哪些职员可以使快乐指数最大
* // 返回最大的快乐指数。
* // 测试链接 : https://www.luogu.com.cn/problem/P1352
* // 本题和讲解037的题目7类似
* // 链式链接 : https://leetcode.cn/problems/house-robber-iii/
* @author: zs宝
* @create: 2025-09-19 11:12
* @Version 1.0
**/public class Code05_Dancing {
public static int MAXN=6001;
//记录员工快乐值
public static int[]nums=new int[MAXN];
//链式前向星建图
public static int[]head=new int[MAXN];
public static int[]next=new int[MAXN];
public static int[]to=new int[MAXN];
public static int cnt;
//判断谁是老板
public static boolean[]boss=new boolean[MAXN];
//判断每个节点要与不要能获得的最大快乐值
// 动态规划表
// yes[i] : i为头的整棵树,在i来的情况下,整棵树能得到的最大快乐值
public static int[]yes=new int[MAXN];
// 动态规划表
// no[i] : i为头的整棵树,在i不来的情况下,整棵树能得到的最大快乐值
public static int[]no=new int[MAXN];
public static int n;
public static int boss_one;
public static void build(){
Arrays.fill(head,0,n+1,0);
Arrays.fill(boss,0,n+1,true);
cnt=1;
}
public static void addEdge(int u,int v){
next[cnt]=head[u];
to[cnt]=v;
head[u]=cnt++;
}
public static void main(String[] args) throws IOException {
BufferedReader buffer=new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in=new StreamTokenizer(buffer);
PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken()!=StreamTokenizer.TT_EOF){
n=(int)in.nval;
build();
for(int i=1;i<=n;i++){
in.nextToken();
nums[i]=(int)in.nval;
}
for(int i=1,u,v;i<n;i++){
in.nextToken();
v=(int)in.nval;
in.nextToken();
u=(int)in.nval;
addEdge(u,v);
boss[v]=false;
}
//找到boss
for(int i=1;i<=n;i++){
if(boss[i]){
boss_one=i;
break;
}
}
f(boss_one);
out.println(Math.max(yes[boss_one],no[boss_one]));
}
out.flush();
out.close();
buffer.close();
}
public static void f(int current){
yes[current]=nums[current];
no[current]=0;
//遍历当前节点的所有员工
for(int ei=head[current],emplyee;ei>0;ei=next[ei]){
emplyee=to[ei];
f(emplyee);
yes[current]+=no[emplyee];
no[current]+=Math.max(yes[emplyee],no[emplyee]);
}
}
}6、监控二叉树
题目描述: 给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
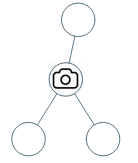
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
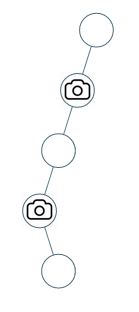
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
给定树的节点数的范围是
[1, 1000]。每个节点的值都是 0。
解题思路:
这个题主要就是讨论清楚可能的状况
主要时要从树的底往上讨论
空节点该怎算呢,只能算覆盖呀,那么这样一来在一个摄像头没加之前,每个叶子节点开始都是子节点被覆盖了,但是当前节点没有被覆盖,这样的话,讨论的范围就是已经预定好子节点被覆盖了,然后推出其它状态
0:当前节点没有被覆盖,但是子节点已经全部覆盖,
1:当前节点被覆盖,子节点也被覆盖,摄像头未在当前节点上
2:当前节点被覆盖了,子节点也被覆盖了,摄像头在当前节点上
代码如下:
package main.java.class078;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code06_BinaryTreeCameras
* @description: 监控二叉树
* // 给定一个二叉树,我们在树的节点上安装摄像头
* // 节点上的每个摄影头都可以监视其父对象、自身及其直接子对象
* // 计算监控树的所有节点所需的最小摄像头数量
* // 测试链接 : https://leetcode.cn/problems/binary-tree-cameras/
* @author: zs宝
* @create: 2025-09-20 10:23
* @Version 1.0
**/public class Code06_BinaryTreeCameras {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public static int ans;
public static int minCameraCover(TreeNode root) {
ans=0;
if(f(root)==0){
ans++;
}
return ans;
}
//假设当前节点上方一定有父节点
//这里我们对摄像头当前节点状态做分类讨论
//0:当前节点没有被覆盖,但是子节点已经全部覆盖,
//1:当前节点被覆盖,子节点也被覆盖,摄像头未在当前节点上
//2:当前节点被覆盖了,子节点也被覆盖了,摄像头在当前节点上
public static int f(TreeNode x){
//3种分类讨论其实都是沿着叶子节点下的空节点慢慢网上推来的
//空节点该怎算呢,只能算覆盖呀,那么这样一来,
//在一个摄像头没加之前,每个叶子节点开始都是子节点被覆盖了,但是当前节点没有被覆盖--0状态
//然后由底到顶的推出1,2的可能性
if(x==null){
return 1;
}
int left=f(x.left);
int right=f(x.right);
//分类讨论当前节点的情况
if(left==0 || right==0){
ans++;
return 2;
}
if(left==1 && right==1){
return 0;
}
return 1;
}
}
}7、路径总和Ⅲ
题目描述: 给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:

输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
提示:
二叉树的节点个数的范围是
[0,1000]-109 <= Node.val <= 109-1000 <= targetSum <= 1000
解题思路:
这个题主要在于题目说的是路径方向必须是向下的,要找到目标和,那就可以算出每个节点的前缀和preSUm,然后找到preSum-targetSum的前缀个数
同时要注意回朔,否则可能出现其它枝丫的preSum-targetSum的前缀
代码如下
package main.java.class078;
import java.util.HashMap;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code07_PathSumIII
* @description: 路径总和 III
* // 给定一个二叉树的根节点 root ,和一个整数 targetSum
* // 求该二叉树里节点值之和等于 targetSum 的 路径 的数目
* // 路径 不需要从根节点开始,也不需要在叶子节点结束
* // 但是路径方向必须是向下的(只能从父节点到子节点)
* // 测试链接 : https://leetcode.cn/problems/path-sum-iii/
* @author: zs宝
* @create: 2025-09-20 11:05
* @Version 1.0
**/public class Code07_PathSumIII {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
//树的前缀和如何表示
//前缀和的回朔,避免计算到不相干的两条分路上的枝丫
public static int ans;
public int pathSum(TreeNode root, int targetSum) {
HashMap<Long,Integer> map=new HashMap<>();
map.put(0L,1);
ans=0;
f(root,targetSum,0L,map);
return ans;
}
public static void f(TreeNode x, int targetSum,Long preSum,HashMap<Long,Integer>map){
if(x==null){
return;
}
//当前节点前缀和
preSum+=x.val;
ans+=map.getOrDefault(preSum-targetSum,0);
map.put(preSum,map.getOrDefault(preSum,0)+1);
f(x.left,targetSum,preSum,map);
f(x.right,targetSum,preSum,map);
//回朔
map.put(preSum,map.get(preSum)-1);
}
}
}