核心思想
树型dp套路
1)分析父树得到答案需要子树的哪些信息
2)把子树信息的全集定义成递归返回值
3)通过递归让子树返回全集信息(一般的递归就是看要不要考虑当前节点)
4)整合子树的全集信息得到父树的全集信息并返回
dfn序 用深度优先遍历的方式遍历整棵树 给每个节点依次标记序号 编号从小到大的顺序就是dfn序 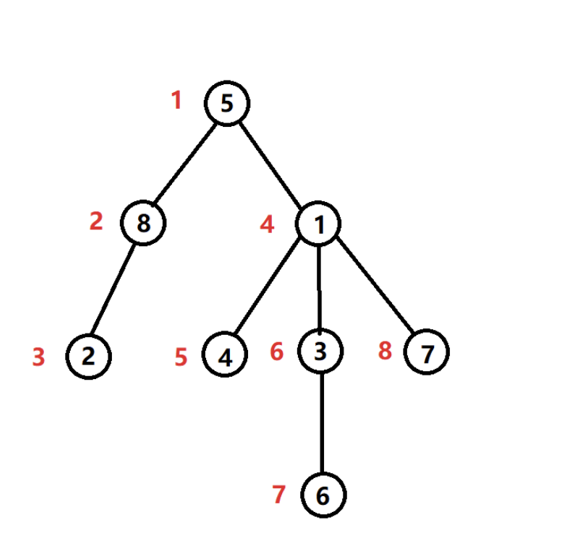
dfn序 + 每颗子树的大小,可以起到定位子树节点的作用 如果某个节点的dfn序号是x,以这个节点为头的子树大小为y 那么可知,dfn序号从x ~ x+y-1所代表的节点,都属于这个节点的子树 利用这个性质, 节点间的关系判断(题目3、4),跨子树的讨论(题目5) 就会变得方便
例题
1、到达首都的最少油耗
题目描述: 给你一棵 n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 到 n - 1 ,且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ,其中 roads[i] = [ai, bi] ,表示城市 ai 和 bi 之间有一条 双向路 。
每个城市里有一个代表,他们都要去首都参加一个会议。
每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。
城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。
请你返回到达首都最少需要多少升汽油。
示例 1:
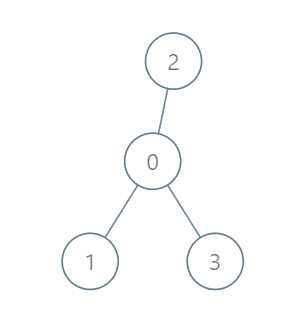
输入:roads = [[0,1],[0,2],[0,3]], seats = 5 输出:3 解释:
代表 1 直接到达首都,消耗 1 升汽油。
代表 2 直接到达首都,消耗 1 升汽油。
代表 3 直接到达首都,消耗 1 升汽油。 最少消耗 3 升汽油。
示例 2:
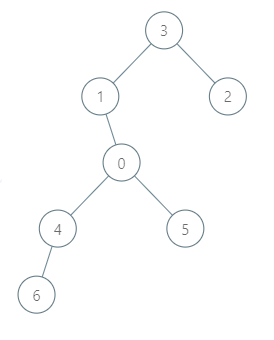
输入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2 输出:7 解释:
代表 2 到达城市 3 ,消耗 1 升汽油。
代表 2 和代表 3 一起到达城市 1 ,消耗 1 升汽油。
代表 2 和代表 3 一起到达首都,消耗 1 升汽油。
代表 1 直接到达首都,消耗 1 升汽油。
代表 5 直接到达首都,消耗 1 升汽油。
代表 6 到达城市 4 ,消耗 1 升汽油。
代表 4 和代表 6 一起到达首都,消耗 1 升汽油。 最少消耗 7 升汽油。
示例 3:

输入:roads = [], seats = 1 输出:0 解释:没有代表需要从别的城市到达首都。
提示:
1 <= n <= 105roads.length == n - 1roads[i].length == 20 <= ai, bi < nai != biroads表示一棵合法的树。1 <= seats <= 105
解题思路:
这个题和上一章 078、树型dp-上的都很类似,树型dp的基本思路,但是这个题由于给的是无向图,我们不知道谁是谁的父节点
所以这个踢在递归的时候有所改变,每次递归带上之前调用递归而来的父节点,避免无向图找路的时候找到走过的节点
其余根据树型dp基本思路,这个题只需要子树节点个数,代价即可
代码如下
package main.java.class079;
import java.util.ArrayList;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code01_MinimumFuelCost
* @description: 到达首都的最少油耗
* // 给你一棵 n 个节点的树(一个无向、连通、无环图)
* // 每个节点表示一个城市,编号从 0 到 n - 1 ,且恰好有 n - 1 条路
* // 0 是首都。给你一个二维整数数组 roads
* // 其中 roads[i] = [ai, bi] ,表示城市 ai 和 bi 之间有一条 双向路
* // 每个城市里有一个代表,他们都要去首都参加一个会议
* // 每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目
* // 城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车
* // 相邻城市之间一辆车的油耗是一升汽油
* // 请你返回到达首都最少需要多少升汽油
* // 测试链接 : https://leetcode.cn/problems/minimum-fuel-cost-to-report-to-the-capital/
* @author: zs宝
* @create: 2025-09-24 09:36
* @Version 1.0
**/public class Code01_MinimumFuelCost {
class Solution {
public long minimumFuelCost(int[][] roads, int seats) {
int n=roads.length+1;
//建图过程
ArrayList<ArrayList<Integer>> graph=new ArrayList<>();
for(int i=0;i<n;i++){
graph.add(new ArrayList<>());
}
for(int[]path:roads){
int u=path[0];
int v=path[1];
graph.get(u).add(v);
graph.get(v).add(u);
}
int[]szie=new int[n];
long[]cost=new long[n];
//开始树型dp
f(graph,0,-1,seats,szie,cost);
return cost[0];
}
/**
u:当前节点
p:当前节点但是父节点
*/
public void f(ArrayList<ArrayList<Integer>> graph,int u,int p,int seats,int[]size,long[]cost){
size[u]=1;
for(int v:graph.get(u)){
//由于是无向图,避免其往走过的节点走
if(p!=v){
f(graph,v,u,seats,size,cost);
size[u]+=size[v];
cost[u]+=cost[v];
cost[u]+=(size[v]+seats-1)/seats;
}
}
}
}
}2、相邻字符不同的最长路径
题目描述: 给你一棵 树(即一个连通、无向、无环图),根节点是节点 0 ,这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父节点,由于节点 0 是根节点,所以 parent[0] == -1 。
另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
示例 1:

输入:parent = [-1,0,0,1,1,2], s = "abacbe" 输出:3 解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3 。 可以证明不存在满足上述条件且比 3 更长的路径。
示例 2:

输入:parent = [-1,0,0,0], s = "aabc" 输出:3 解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3 。
提示:
n == parent.length == s.length1 <= n <= 105对所有
i >= 1,0 <= parent[i] <= n - 1均成立parent[0] == -1parent表示一棵有效的树s仅由小写英文字母组成
解题思路:
这个题仍然是一个基础的树型dp流程
但是这个题,我在看到parent这种告诉父节点的时候,一下子不知道改如何建图了
其余就和以往的树找最长路径几乎相同
每次分析树的最长路径时,在递归方面由于根节点有多个子树,因此总会考虑,路径包含根节点,路径不包含根节点(要么完全在某个子树中(不经过当前节点),要么经过当前节点,从该节点往下走两条分支拼成,)
而每一个包含根节点的路径其实是由2个子树的从子树根节点开始往下进行深度遍历的路径组合(这种组合都会考虑题意条件)
维护 从它往下的最长链(子问题),再看经过它的两条最长链拼接能不能刷新全局最大值。
所以最终的最长路径(子树的最大路径,2个符合题意的子树的最大深度+1)
本题需要的变量为
必须从头节点出发的最长路径
当前子树的最长路径
代码如下:
package main.java.class079;
import java.util.ArrayList;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code02_LongestPathWithDifferentAdjacent
* @description: 相邻字符不同的最长路径
* // 给你一棵 树(即一个连通、无向、无环图),根节点是节点 0
* // 这棵树由编号从 0 到 n - 1 的 n 个节点组成
* // 用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树
* // 其中 parent[i] 是节点 i 的父节点
* // 由于节点 0 是根节点,所以 parent[0] == -1
* // 另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符
* // 请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径
* // 并返回该路径的长度
* // 测试链接 : https://leetcode.cn/problems/longest-path-with-different-adjacent-characters/
* @author: zs宝
* @create: 2025-09-24 10:14
* @Version 1.0
**/public class Code02_LongestPathWithDifferentAdjacent {
class Solution {
public static int longestPath(int[] parent, String str) {
int n=parent.length;
ArrayList<ArrayList<Integer>> graph=new ArrayList<>();
for(int i=0;i<n;i++){
graph.add(new ArrayList<>());
}
for(int i=1;i<n;i++){
graph.get(parent[i]).add(i);
}
char[]s=str.toCharArray();
return f(graph,0,s).maxPath;
}
public static class info{
//必须从头节点出发的最长路径
int maxFromHead;
//当前子树的最长路径
int maxPath;
public info(int a,int b){
maxFromHead=a;
maxPath=b;
}
}
public static info f(ArrayList<ArrayList<Integer>> graph, int u, char[]s){
if(graph.get(u).isEmpty()){
return new info(1,1);
}
//树的最长路径分为两种讨论,经过根节点,不经过根节点
//而经过根节点的话,最长的就是其子树中两个最长的从根节点(子树的)出发的路径之和加上根节点
//因此为了寻找这个两个子树从根节点出发的最长路径,就需要有两个变量,最长和次长
//同时结合题意相邻节点的字符不同
int max1=0;
int max2=0;
int maxPath=1;
for(int v:graph.get(u)){
info inf=f(graph,v,s);
maxPath=Math.max(maxPath,inf.maxPath);
//寻找最长和次长的过程
if(s[v]!=s[u]){
if(inf.maxFromHead>max1){
max2=max1;
max1=inf.maxFromHead;
}else if(inf.maxFromHead>max2){
max2=inf.maxFromHead;
}
}
}
int maxFromHead=max1+1;
maxPath=Math.max(maxPath,max1+max2+1);
return new info(maxFromHead,maxPath);
}
}
}3、移除子树后的二叉树高度
题目描述: 给你一棵 二叉树 的根节点 root ,树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。
你必须在树上执行 m 个 独立 的查询,其中第 i 个查询你需要执行以下操作:
从树中 移除 以
queries[i]的值作为根节点的子树。题目所用测试用例保证queries[i]不 等于根节点的值。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是执行第 i 个查询后树的高度。
注意:
查询之间是独立的,所以在每个查询执行后,树会回到其 初始 状态。
树的高度是从根到树中某个节点的 最长简单路径中的边数 。
示例 1:
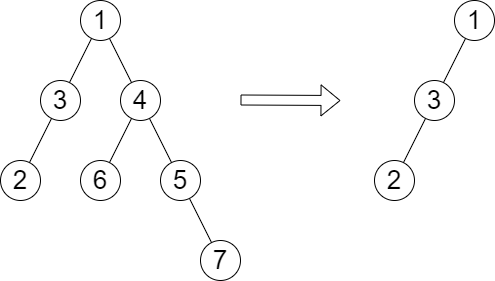
输入:root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4] 输出:[2] 解释:上图展示了从树中移除以 4 为根节点的子树。 树的高度是 2(路径为 1 -> 3 -> 2)。
示例 2:
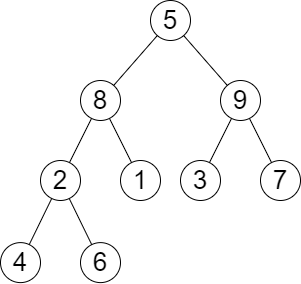
输入:root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8] 输出:[3,2,3,2] 解释:执行下述查询:
移除以 3 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 4)。
移除以 2 为根节点的子树。树的高度变为 2(路径为 5 -> 8 -> 1)。
移除以 4 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 6)。
移除以 8 为根节点的子树。树的高度变为 2(路径为 5 -> 9 -> 3)。
提示:
树中节点的数目是
n2 <= n <= 1051 <= Node.val <= n树中的所有值 互不相同
m == queries.length1 <= m <= min(n, 104)1 <= queries[i] <= nqueries[i] != root.val
解题思路:
其实这道题一眼看过去思路很清楚,就是树型dp找出每个节点的为根节点子树的大小,当前节点的深度,在每次去掉以某个节点为根节点的子树后,排除这些子树节点的剩余节点中,深度最大的为多少,即可
但是这里有个问题的是,由于是树的结构,每个节点我们无法标记,哪怕val值不同,但是val值的不连续,导致我们在对某一个节点为根节点的时候其size对应的子树节点有那些在只有size时是无法确定的。若要再用一个结构去存储,那么每次递归时就要收集,每次排除子树节点时也要查询,根据数据量,这个时间复杂度很难通过
因此这里我们采用dfn序,用dfn序来将对应的子树节点的序号连续,这样就可以很方便的通过size确定那些节点是其的子树
然后构造辅助数组,一个记录从左往右的节点的最大深度,一个从右往左记录。方便去掉以某个节点为根节点的子树后快速查询最大深度。
代码如下:
package main.java.class079;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code03_HeightRemovalQueries
* @description: 移除子树后的二叉树高度
* // 给你一棵 二叉树 的根节点 root ,树中有 n 个节点
* // 每个节点都可以被分配一个从 1 到 n 且互不相同的值
* // 另给你一个长度为 m 的数组 queries
* // 你必须在树上执行 m 个 独立 的查询,其中第 i 个查询你需要执行以下操作:
* // 从树中 移除 以 queries[i] 的值作为根节点的子树
* // 题目所用测试用例保证 queries[i] 不等于根节点的值
* // 返回一个长度为 m 的数组 answer
* // 其中 answer[i] 是执行第 i 个查询后树的高度
* // 注意:
* // 查询之间是独立的,所以在每个查询执行后,树会回到其初始状态
* // 树的高度是从根到树中某个节点的 最长简单路径中的边数
* // 测试链接 : https://leetcode.cn/problems/height-of-binary-tree-after-subtree-removal-queries/
* @author: zs宝
* @create: 2025-09-24 11:24
* @Version 1.0
**/public class Code03_HeightRemovalQueries {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public static int MAXN=100011;
//记录每个节点的dfn序是多少
//以节点的val值为下标
public static int[]dfn=new int[MAXN];
//记录每个dfn序的节点的深度是多少(以这个节点为叶子节点)
//下标为dfn序
public static int[]deeep=new int[MAXN];
//记录以每个dfn序为根节点的子树大小
public static int[]size=new int[MAXN];
//记录当前dfn序前的序号为为叶子节点可以得到的最大深度
public static int[]maxl=new int[MAXN];
//记录当前dfn序后的序号为叶子节点可以得到的最大深度
public static int[]maxr=new int[MAXN];
//dfn序号
public static int dfnCnt;
public static int[] treeQueries(TreeNode root, int[] queries) {
dfnCnt=0;
f(root,0);
for(int i=1;i<=dfnCnt;i++){
maxl[i]=Math.max(maxl[i-1],deeep[i]);
}
maxr[dfnCnt+1]=0;
for(int i=dfnCnt;i>=1;i--){
maxr[i]=Math.max(maxr[i+1],deeep[i]);
}
int m=queries.length;
int[] ans=new int[m];
for(int i=0,df;i<m;i++){
df=dfn[queries[i]];
ans[i]=Math.max(maxl[df-1],maxr[df+size[df]]);
}
return ans;
}
/**
x:为当前节点
k:为当前深度
*/
public static void f(TreeNode x,int k){
int i=++dfnCnt;
dfn[x.val]=i;
deeep[i]=k;
size[i]=1;
if(x.left!=null){
f(x.left,k+1);
size[i]+=size[dfn[x.left.val]];
}
if(x.right!=null){
f(x.right,k+1);
size[i]+=size[dfn[x.right.val]];
}
}
}
}4、从树中删除边的最小分数
题目描述: 存在一棵无向连通树,树中有编号从 0 到 n - 1 的 n 个节点, 以及 n - 1 条边。
给你一个下标从 0 开始的整数数组 nums ,长度为 n ,其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。
删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案,定义如下步骤以计算其分数:
分别获取三个组件 每个 组件中所有节点值的异或值。
最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。
例如,三个组件的节点值分别是:
[4,5,7]、[1,9]和[3,3,3]。三个异或值分别是4 ^ 5 ^ 7 = _**6**_、1 ^ 9 = _**8**_和3 ^ 3 ^ 3 = _**3**_。最大异或值是8,最小异或值是3,分数是8 - 3 = 5。
返回在给定树上执行任意删除边方案可能的 最小 分数。
示例 1:
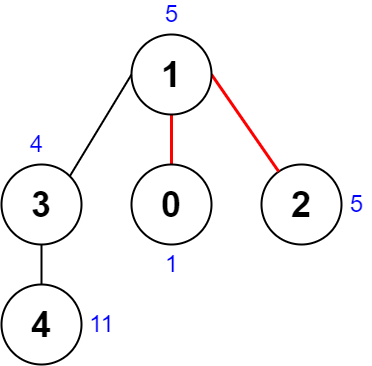
输入:nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]] 输出:9 解释:上图展示了一种删除边方案。
第 1 个组件的节点是 [1,3,4] ,值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
第 2 个组件的节点是 [0] ,值是 [1] 。异或值是 1 = 1 。
第 3 个组件的节点是 [2] ,值是 [5] 。异或值是 5 = 5 。 分数是最大异或值和最小异或值的差值,10 - 1 = 9 。 可以证明不存在分数比 9 小的删除边方案。
示例 2:
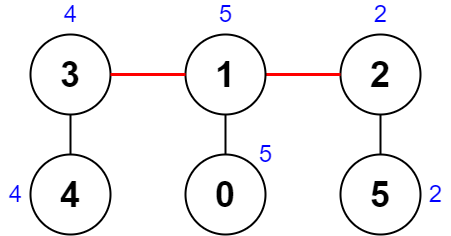
输入:nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]] 输出:0 解释:上图展示了一种删除边方案。
第 1 个组件的节点是 [3,4] ,值是 [4,4] 。异或值是 4 ^ 4 = 0 。
第 2 个组件的节点是 [1,0] ,值是 [5,5] 。异或值是 5 ^ 5 = 0 。
第 3 个组件的节点是 [2,5] ,值是 [2,2] 。异或值是 2 ^ 2 = 0 。 分数是最大异或值和最小异或值的差值,0 - 0 = 0 。 无法获得比 0 更小的分数 0 。
提示:
n == nums.length3 <= n <= 10001 <= nums[i] <= 108edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树
解题思路:
这个题在做的时候我陷入了一种矛盾,我不知道该怎么建图,我想到过用邻接表建图,但是邻接表建图后,这个dfn序如何设置,由于是无向连通图,我该如何知道某个节点是否已经遍历过了,不知道为啥, 就一直卡在这
最后可以先将所有dfn序初始为0,为0的就是没有遍历过的。这是由于图的节点序号为dfn数组的下标
然后根据异或计算的特性a^b=c, 那么a^c=b, b^c=a。
那么有dfn序就可以很容易的知道其子树节点的范围,那么可以再键一个数组专门保存以某个节点为根节点的子树的节点异或值
接下来就是循环尝试不同的2条边带来的效果,这个没有办法,只能每种可能都尝试一下
但是要在其中注意选择的两条边产生的两颗子树,需要讨论
第二课子树是从第一课子树中出来的,即第二课子树原本是另一条变划分出来子树的子树
第二课子树不是从第一课子树中出来的,即第二课子树不·是另一条变划分出来子树的子树
最后分别求3颗树的异或值
代码如下
package main.java.class079;
import java.util.ArrayList;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code04_MinimumScoreAfterRemovals
* @description: 从树中删除边的最小分数
* // 存在一棵无向连通树,树中有编号从0到n-1的n个节点,以及n-1条边
* // 给你一个下标从0开始的整数数组nums长度为n,其中nums[i]表示第i个节点的值
* // 另给你一个二维整数数组edges长度为n-1
* // 其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边
* // 删除树中两条不同的边以形成三个连通组件,对于一种删除边方案,定义如下步骤以计算其分数:
* // 分别获取三个组件每个组件中所有节点值的异或值
* // 最大 异或值和 最小 异或值的 差值 就是这种删除边方案的分数
* // 返回可能的最小分数
* // 测试链接 : https://leetcode.cn/problems/minimum-score-after-removals-on-a-tree/
* @author: zs宝
* @create: 2025-09-25 10:20
* @Version 1.0
**/public class Code04_MinimumScoreAfterRemovals {
class Solution {
public static int MAXN=1001;
public static int[]dfn=new int[MAXN];
//以当前节点为根节点的子树的异或值
public static int[]xor=new int[MAXN];
public static int[]size=new int[MAXN];
public static int dfnCnt;
public static int minimumScore(int[] nums, int[][] edges) {
int n=nums.length;
//先建图
ArrayList<ArrayList<Integer>> graph=new ArrayList<>();
for(int i=0;i<n;i++){
graph.add(new ArrayList<>());
}
for(int []edge:edges){
int u=edge[0];
int v=edge[1];
graph.get(u).add(v);
graph.get(v).add(u);
}
//构建dfn序
dfnCnt=0;
Arrays.fill(dfn,0,n,0);
f(graph,nums,0);
//接下来开始分配边,2条边
int m=edges.length;
int ans=Integer.MAX_VALUE;
for(int i=0,a,b,pre,pos,sum1,sum2,sum3;i<m;i++){
//找到由两条边划分的子树的2个根节点
a=Math.max(dfn[edges[i][0]],dfn[edges[i][1]]);
for(int j=i+1;j<m;j++){
b=Math.max(dfn[edges[j][0]],dfn[edges[j][1]]);
//两个根节点dfn序小的为pre,大的为pos
if(a<b){
pre=a;
pos=b;
}else{
pre=b;
pos=a;
}
//若划分的根节点,pos为pre子树中的节点
if(pre+size[pre]>pos){
//sum1以划分边中以较小dfn序号为根节点的子树异或值
//sum2以划分边中以较大dfn序号为根节点的子树异或值
//sum3以总树减去由划分两条边的子树节点,剩余节点的异或值
sum2=xor[pos];
sum1=xor[pre]^xor[pos];
sum3=xor[1]^xor[pre];
}else{
//若划分的根节点,pos不是pre子树中的节点
sum2=xor[pos];
sum1=xor[pre];
sum3=xor[1]^xor[pos]^xor[pre];
}
ans=Math.min(ans,Math.max(sum1,Math.max(sum2,sum3))-Math.min(sum1,Math.min(sum2,sum3)));
}
}
return ans;
}
public static void f(ArrayList<ArrayList<Integer>> graph, int[]nums, int u){
int i=++dfnCnt;
dfn[u]=i;
xor[i]=nums[u];
size[i]=1;
//根据它的边继续构建
for(int v:graph.get(u)){
//如果这个节点还没有分配dfn序,则开始分配
//dfn序初始化为0,不为0说明已经走过了这个节点
if(dfn[v]==0){
f(graph,nums,v);
xor[i]^=xor[dfn[v]];
size[i]+=size[dfn[v]];
}
}
}
}
}5、选课
题目描述:
在大学里每个学生,为了达到一定的学分,必须从很多课程里选择一些课程来学习,在课程里有些课程必须在某些课程之前学习,如高等数学总是在其它课程之前学习。现在有 N 门功课,每门课有若干学分,分别记作 s_1,s_2,\cdots,s_N,每门课有一门或没有直接先修课(若课程 a 是课程 b 的先修课即只有学完了课程 a,才能学习课程 b)。一个学生要从这些课程里选择 M 门课程学习,问他能获得的最大学分是多少?
输入格式
第一行有两个整数 N,M 用空格隔开 (1 \leq N \leq 300 , 1 \leq M \leq 300)。
接下来的 N 行, 第 i+1 行包含两个整数 k_i 和 s_i, k_i 表示第 i 门课的直接先修课,s_i 表示第 i 门课的学分。若 k_i=0 表示没有直接先修课 (0 \leq {k_i} \leq N, 1 \leq {s_i} \leq 20)。
输出格式
只有一行,选 M 门课程的最大学分。
输入输出样例 #1
输入 #1
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2输出 #1
13解题思路
请参考左程云-算法通关系列-079-树型dp下
代码如下 普通解法
package main.java.class079;
import java.io.*;
import java.util.ArrayList;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code05_CourseSelection1
* @description: 选课
* // 在大学里每个学生,为了达到一定的学分,必须从很多课程里选择一些课程来学习
* // 在课程里有些课程必须在某些课程之前学习,如高等数学总是在其它课程之前学习
* // 现在有 N 门功课,每门课有个学分,每门课有一门或没有直接先修课
* // 若课程 a 是课程 b 的先修课即只有学完了课程 a,才能学习课程 b
* // 一个学生要从这些课程里选择 M 门课程学习
* // 问他能获得的最大学分是多少
* // 测试链接 : https://www.luogu.com.cn/problem/P2014
* @author: zs宝
* @create: 2025-09-25 19:43
* @Version 1.0
**/// 普通解法,邻接表建图 + 相对好懂的动态规划
// 几乎所有题解都是普通解法的思路,只不过优化了常数时间、做了空间压缩
// 但时间复杂度依然是O(n * 每个节点的孩子平均数量 * m的平方)
public class Code05_CourseSelection1 {
public static int MAXN=301;
public static int n,m;
public static int[]credit=new int[MAXN];
public static ArrayList<ArrayList<Integer>> graph;
static {
graph = new ArrayList<>();
for (int i = 0; i < MAXN; i++) {
graph.add(new ArrayList<>());
}
}
public static void build(){
for(int i=0;i<=n;i++){
graph.get(i).clear();
}
}
public static int[][][]dp=new int[MAXN][][];
public static void main(String[] args) throws IOException {
BufferedReader buffer=new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in=new StreamTokenizer(buffer);
PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken()!=StreamTokenizer.TT_EOF){
n=(int)in.nval;
in.nextToken();
m=(int)in.nval+1;
build();
for(int i=1,ki,si;i<=n;i++){
in.nextToken();
ki=(int)in.nval;
in.nextToken();
si=(int)in.nval;
credit[i]=si;
//在所有课程节点前面设置一个虚拟的0节点
graph.get(ki).add(i);
}
out.println(compute());
}
out.flush();;
out.close();
buffer.close();
}
//暴力递归的解法
public static int compute(){
for(int i=0;i<=n;i++){
dp[i]=new int[graph.get(i).size()+1][m+1];
}
for(int i=0;i<=n;i++){
for(int j=0;j<dp[i].length;j++){
for(int k=0;k<=m;k++){
dp[i][j][k]=-1;
}
}
}
return f(0,graph.get(0).size(),m);
}
// 当前来到i号节点为头的子树
// 只在i号节点、及其i号节点下方的前j棵子树上挑选节点
// 一共挑选k个节点,并且保证挑选的节点连成一片
// 返回最大的累加和
private static int f(int i, int j, int k) {
if(k==0){
return 0;
}
if(j==0 || k==1){
return credit[i];
}
if(dp[i][j][k]!=-1){
return dp[i][j][k];
}
int ans=f(i,j-1,k);
// 第j棵子树头节点v
int v=graph.get(i).get(j-1);
for(int w=1;w<k;w++){
ans=Math.max(ans,f(v,graph.get(v).size(),w)+f(i,j-1,k-w));
}
dp[i][j][k]=ans;
return ans;
}
}最优解法
package main.java.class079;
import java.io.*;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code05_CourseSelection2
* @description: 选课
* // 在大学里每个学生,为了达到一定的学分,必须从很多课程里选择一些课程来学习
* // 在课程里有些课程必须在某些课程之前学习,如高等数学总是在其它课程之前学习
* // 现在有 N 门功课,每门课有个学分,每门课有一门或没有直接先修课
* // 若课程 a 是课程 b 的先修课即只有学完了课程 a,才能学习课程 b
* // 一个学生要从这些课程里选择 M 门课程学习
* // 问他能获得的最大学分是多少
* // 测试链接 : https://www.luogu.com.cn/problem/P2014
* @author: zs宝
* @create: 2025-09-25 20:24
* @Version 1.0
**/// 最优解,链式前向星建图 + dfn序的利用 + 巧妙定义下的尝试
// 时间复杂度O(n*m),觉得难可以跳过,这个最优解是非常巧妙和精彩的!
public class Code05_CourseSelection2 {
public static int MAXN=301;
public static int[]nums=new int[MAXN];
//链式前向星建图
public static int cnt;
public static int[]head=new int[MAXN];
public static int[]next=new int[MAXN];
public static int[]to=new int[MAXN];
//构建dfn序
public static int dfnCnt;
public static int[]val=new int[MAXN+1];
public static int[]size=new int[MAXN+1];
public static int[][]dp=new int[MAXN+2][MAXN];
public static int n,m;
public static void main(String[] args) throws IOException {
BufferedReader buffer=new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in=new StreamTokenizer(buffer);
PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken()!=StreamTokenizer.TT_EOF){
n=(int)in.nval;
in.nextToken();
m=(int)in.nval;
build();
for(int i=1,ki,si;i<=n;i++){
in.nextToken();
ki=(int)in.nval;
in.nextToken();
si=(int)in.nval;
nums[i]=si;
addEdge(ki,i);
}
out.println(compute());
}
out.flush();;
out.close();
buffer.close();
}
public static void build(){
dfnCnt=0;
cnt=1;
Arrays.fill(head,0,n+1,0);
Arrays.fill(dp[n+2],0,m+1,0);
}
public static void addEdge(int u,int v){
next[cnt]=head[u];
to[cnt]=v;
head[u]=cnt++;
}
public static int compute(){
f(0);
// 节点编号0 ~ n,dfn序号范围1 ~ n+1
// 接下来的逻辑其实就是01背包!不过经历了很多转化
// 整体的顺序是根据dfn序来进行的,从大的dfn序,遍历到小的dfn序
// dp[i][j] : i ~ n+1 范围的节点,选择j个节点一定要形成有效结构的情况下,最大的累加和
// 怎么定义有效结构?重点!重点!重点!
// 假设i ~ n+1范围上,目前所有头节点的上方,有一个总的头节点
// i ~ n+1范围所有节点,选出来j个节点的结构,
// 挂在这个假想的总头节点之下,是一个连续的结构,没有断开的情况
// 那么就说,i ~ n+1范围所有节点,选出来j个节点的结构是一个有效结构
for(int i=n+1;i>=2;i--){
for(int j=1;j<=m;j++){
dp[i][j]=Math.max(dp[i+size[i]][j],dp[i+1][j-1]+val[i]);
}
}
// dp[2][m] : 2 ~ n范围上,选择m个节点一定要形成有效结构的情况下,最大的累加和
// 最后来到dfn序为1的节点,一定是原始的0号节点
// 原始0号节点下方一定挂着有效结构
// 并且和补充的0号节点一定能整体连在一起,没有任何跳跃连接
// 于是整个问题解决
return nums[0]+dp[2][m];
}
//dfn的构建
public static int f(int u){
int i=++dfnCnt;
val[i]=nums[u];
size[i]=1;
for(int ei=head[u],v;ei>0;ei=next[ei]){
v=to[ei];
size[i]+=f(v);
}
return size[i];
}
}