核心思想

上章节讲了利用严格位置依赖的动态规划来建立空间感，进而观察并优化枚举

本章节继续观察并优化转移方程来优化枚举（题目1、2）同时还要观察并设计高效的查询结构来优化枚举（题目3、4）

例题

1、规划兼职工作

题目描述：你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i] 结束，报酬为 profit[i]。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

示例 1：

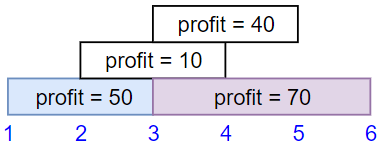
输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70] 输出：120 解释： 我们选出第 1 份和第 4 份工作，时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。

示例 2：

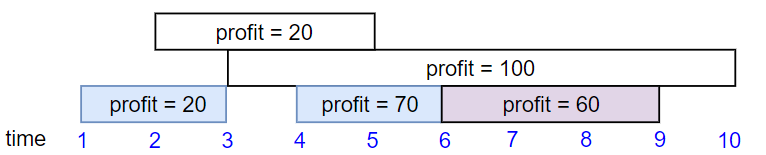
输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60] 输出：150 解释： 我们选择第 1，4，5 份工作。共获得报酬 150 = 20 + 70 + 60。

示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4] 输出：6

提示：

1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4

解题思路：

先按照兼职结束时间对兼职排序
对于每一个兼职都有做与不做的选择性判断。
每种判断都要顾及选择兼职的结束时间和开始时间
其中我在写代码的时候先让 dp[i] 选择了不要第i中兼职，但是这样写在后续的对要第i个兼职的判定进入却有问题。
应该先假设要第i个兼职，最后再与不要进行判段取舍
利用观察单调性 + 二分搜索的方式优化枚举，最优解时间复杂度O (n*logn)

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 1235 + 规划兼职工作
🧠 题目关键词（原文关键词）	每份工作预计从 `startTime[i]` 开始到 `endTime[i]` 结束，报酬为 `profit[i]`，时间上出现重叠的 2 份工作不能同时进行
🧩 抽象问题类型（题目本质）	类似背包问题
🔍 数据规模 / 限制	- `1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4` - `1 <= startTime[i] < endTime[i] <= 10^9` - `1 <= profit[i] <= 10^4`
🧭 我的初步思路	动态规划
✅ 正确解法类型	动态规划
❗ 没想到的原因	代码写错
📦 归入的题型分类	动态规划类
🧠 触发词（以后遇到就联想）	规划兼职->动态规划
🧪 解法一句话总结	先按照兼职结束时间对兼职排序，然后转为01背包的思路要与不要，注意要的时候对时间不能有重叠的要求

代码如下

 package main.java.class083;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code01_MaximumProfitInJobScheduling  
  * @description: 规划兼职工作  
  * // 你打算利用空闲时间来做兼职工作赚些零花钱，这里有n份兼职工作  
  * // 每份工作预计从startTime[i]开始、endTime[i]结束，报酬为profit[i]  
  * // 返回可以获得的最大报酬  
  * // 注意，时间上出现重叠的 2 份工作不能同时进行  
  * // 如果你选择的工作在时间X结束，那么你可以立刻进行在时间X开始的下一份工作  
  * // 测试链接 : https://leetcode.cn/problems/maximum-profit-in-job-scheduling/  
  * @author: zs宝  
  * @create: 2025-10-07 11:01  
  * @Version 1.0  
  **/public class Code01_MaximumProfitInJobScheduling {  
     class Solution {  
         public static int MAXN=500001;  
         public static int[][]jobs=new int[MAXN][3];  
         public static int[]dp=new int[MAXN];  
         public static int jobScheduling(int[] startTime, int[] endTime, int[] profits) {  
             int n=startTime.length;  
             for(int i=0;i<n;i++){  
                 jobs[i][0]=startTime[i];  
                 jobs[i][1]=endTime[i];  
                 jobs[i][2]=profits[i];  
             }  
             //根据兼职结束时间从小到达排列  
             Arrays.sort(jobs,0,n,(a,b)->a[1]-b[1]);  
             //接下来开始dp，要或者不要第i个兼职  
             dp[0]=jobs[0][2];  
             for(int i=1,start,profit,fd;i<n;i++){  
                 start=jobs[i][0];  
                 profit=jobs[i][2];  
                 //要第i个兼职  
                 dp[i]=profit;  
                 //开始计算要第i个兼职的  
                 //寻找里当前兼职的开始时间最近的那个兼职（这个兼职的结束时间要在开始时间之前）  
                 if(jobs[0][1]<=start){  
                     fd=find(i-1,start);  
                     dp[i]+=dp[fd];  
                 }  
                 //要与不要做判断  
                 dp[i]=Math.max(dp[i],dp[i-1]);  
             }  
             return dp[n-1];  
         }  
   
         public static int find(int i,int time){  
             int l=0;  
             int r=i;  
             int m=0;  
             int ans=0;  
             while(l<=r){  
                 m=(l+r)/2;  
                 if(jobs[m][1]<=time){  
                     l=m+1;  
                     ans=m;  
                 }else{  
                     r=m-1;  
                 }  
             }  
             return ans;  
         }  
     }  
 }

2、K个逆序对数组

题目描述：对于一个整数数组 nums，逆序对是一对满足 0 <= i < j < nums.length 且 nums[i] > nums[j]的整数对 [i, j] 。

给你两个整数 n 和 k，找出所有包含从 1 到 n 的数字，且恰好拥有 k 个 逆序对 的不同的数组的个数。由于答案可能很大，只需要返回对 109 + 7 取余的结果。

示例 1：

输入：n = 3, k = 0 输出：1 解释： 只有数组 [1,2,3] 包含了从1到3的整数并且正好拥有 0 个逆序对。

示例 2：

输入：n = 3, k = 1 输出：2 解释： 数组 [1,3,2] 和 [2,1,3] 都有 1 个逆序对。

提示：

1 <= n <= 1000
0 <= k <= 1000

解题思路：

定义 dp[i][j]:i个数，且恰好用于j个逆序对的不同的数组个数
这里要针对i, j的大小做分类讨论，主要是第i行的数值与第i-1行有关，我们把第i行最大的数专门提到最后面，跟着j的变化往前挪动，那么由于i的限制（总共才i个数，挪动的次数有限），因此要对i, j的关系讨论
- i>j, dp[i][j] = dp[i-1][0..... j] 之和
- i<j, dp[i][j] = dp[i-1][j-i+1....... j] 之和
注意dp数组对于j=0的位置都为1，dp[0][0]也是，不要忽略（后续的优化版本最开始写就是错在这个地方）
最优解利用观察 + 构造窗口累加和

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 629 + K个逆序对数组
🧠 题目关键词（原文关键词）	逆序对， `1` 到 `n` 的数字，恰好拥有 `k` 个逆序对的不同的数组的个数
🧩 抽象问题类型（题目本质）	逆序对模型
🔍 数据规模 / 限制	- `1 <= n <= 1000` - `0 <= k <= 1000`
🧭 我的初步思路	动态规划
✅ 正确解法类型	动态规划
❗ 没想到的原因	识别出来了，可是忽略了对与0,0位置的初始化
📦 归入的题型分类	动态规划类
🧠 触发词（以后遇到就联想）	逆序对k个->动态规划类
🧪 解法一句话总结	定义 `dp[i][j]`:i个数，且恰好用于j个逆序对的不同的数组个数，对i, j的大小关系分类讨论

代码如下

 package main.java.class083;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code02_KInversePairsArray  
  * @description: K个逆序对数组  
  * // 逆序对的定义如下：  
  * // 对于数组nums的第i个和第j个元素  
  * // 如果满足0<=i<j<nums.length 且 nums[i]>nums[j]，则为一个逆序对  
  * // 给你两个整数n和k，找出所有包含从1到n的数字  
  * // 且恰好拥有k个逆序对的不同的数组的个数  
  * // 由于答案可能很大，答案对 1000000007 取模  
  * // 测试链接 : https://leetcode.cn/problems/k-inverse-pairs-array/  
  * @author: zs宝  
  * @create: 2025-10-07 12:01  
  * @Version 1.0  
  **/public class Code02_KInversePairsArray {  
     class Solution {  
         public static int MOD=1000000007;  
   
         public static int kInversePairs(int n, int k) {  
             return kInversePairs2(n,k);  
         }  
   
   
         //不带枚举优化的版本  
         public static int kInversePairs1(int n, int k) {  
             //dp[i][j]:i个数，且恰好用于j个逆序对的不同的数组个数  
             int[][]dp=new int[n+1][k+1];  
             dp[0][0]=1;  
             for(int i=1;i<=n;i++){  
                 dp[i][0]=1;  
                 for(int j=1;j<=k;j++){  
                     if(i>j){  
                         for(int p=j;p>=0;p--){  
                             dp[i][j]=(dp[i][j]+dp[i-1][p])%MOD;  
                         }  
                     }else{  
                         for(int p=j-i+1;p<=j;p++){  
                             dp[i][j]=(dp[i][j]+dp[i-1][p])%MOD;  
                         }  
                     }  
                 }  
             }  
             return dp[n][k];  
         }  
   
   
         //通过观察法优化枚举:滑动窗口辅助  
         public static int kInversePairs2(int n, int k) {  
             //dp[i][j]:i个数，且恰好用于j个逆序对的不同的数组个数  
             int[][]dp=new int[n+1][k+1];  
             dp[0][0]=1;  
             for(int i=1,w;i<=n;i++){  
                 dp[i][0]=1;  
                 //由于是从j=1开始，但是j=0时是为1的，因此滑动窗口初始为1  
                 w=1;  
                 for(int j=1;j<=k;j++){  
                     if(i>j){  
                         w=(w+dp[i-1][j])%MOD;  
                     }else{  
                         w=(w+dp[i-1][j])%MOD;  
                         w=(w-dp[i-1][j-i]+MOD)%MOD;  
                     }  
                     dp[i][j]=w;  
                 }  
             }  
             return dp[n][k];  
         }  
     }  
 }

3、自由之路

题目描述：电子游戏“辐射4”中，任务 “通向自由” 要求玩家到达名为 “Freedom Trail Ring” 的金属表盘，并使用表盘拼写特定关键词才能开门。

给定一个字符串 ring ，表示刻在外环上的编码；给定另一个字符串 key ，表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。

最初，ring 的第一个字符与 12:00 方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐，然后按下中心按钮，以此逐个拼写完 key 中的所有字符。

旋转 ring 拼出 key 字符 key[i] 的阶段中：

您可以将 ring 顺时针或逆时针旋转 一个位置 ，计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐，并且这个字符必须等于字符 key[i] 。
如果字符 key[i] 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。

示例 1：

输入: ring = "godding", key = "gd" 输出: 4 解释: 对于 key 的第一个字符 'g'，已经在正确的位置, 我们只需要1步来拼写这个字符。对于 key 的第二个字符 'd'，我们需要逆时针旋转 ring "godding" 2步使它变成 "ddinggo"。当然, 我们还需要1步进行拼写。因此最终的输出是 4。

示例 2:

输入: ring = "godding", key = "godding" 输出: 13

提示：

1 <= ring.length, key.length <= 100
ring 和 key 只包含小写英文字母
保证字符串 key 一定可以由字符串 ring 旋转拼出

解题思路：

定义dp[i][j]:当前按钮指向ring的i位置的字符，要去解决key中第j位置的字符
每次寻找离当前位置最近的合适字符，只不过这里要做分类讨论，是顺时针找到的好，还是逆时针找到的好
最后寻找的过程利用二分搜索优化
这里其实是有一点贪心的策略：下一步做枚举时，不需要枚举所有可能性，只需要枚举顺时针的最近、逆时针的最近两种可能性即可

项目名称	内容填写（每道题一行填写）
📘 题目编号 / 标题	LeetCode 514 + 自由之路
🧠 题目关键词（原文关键词）	旋转 `ring` 拼出 key 字符 `key[i]` 的阶段中： 1. 您可以将 ring 顺时针或逆时针旋转一个位置，计为1步。旋转的最终目的是将字符串 `ring` 的一个字符与 `12:00` 方向对齐，并且这个字符必须等于字符 `key[i]` 。 2. 如果字符 `key[i]` 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。
🧩 抽象问题类型（题目本质）	字符匹配
🔍 数据规模 / 限制	- `1 <= ring.length, key.length <= 100` - `ring` 和 `key` 只包含小写英文字母 - 保证字符串 `key` 一定可以由字符串 `ring` 旋转拼出
🧭 我的初步思路	动态规划
✅ 正确解法类型	动态规划
❗ 没想到的原因	想到了，但是在计算旋转的所产生的代价时，误以为时旋转一次代价为1，其实旋转了多少格，代价就为多少
📦 归入的题型分类	动态规划
🧠 触发词（以后遇到就联想）	字符匹配旋转->动态规划+二分查找优化
🧪 解法一句话总结	每次寻找离当前位置最近的合适字符，只不过这里要做分类讨论，是顺时针找到的好，还是逆时针找到的好

我的代码如下

 package main.java.class083;  
   
 import java.util.Arrays;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code03_FreedomTrail  
  * @description: 自由之路  
  * // 题目描述比较多，打开链接查看  
  * // 测试链接 : https://leetcode.cn/problems/freedom-trail/  
  * @author: zs宝  
  * @create: 2025-10-08 10:23  
  * @Version 1.0  
  **/public class Code03_FreedomTrail {  
     class Solution {  
         public static int MAXN=101;  
         public static int MAXC=26;  
         //存储每种字符出现的数量  
         public static int[]size=new int[MAXC];  
         //存储每种字符出现的位置  
         public static int[][]where=new int[MAXC][MAXN];  
   
         //用于存储给定的ring字符  
         public static int[]rings=new int[MAXN];  
   
         //用于存储给定的key字符  
         public static int[]keys=new int[MAXN];  
   
         public static int n,m;  
   
         //dp[i][j]:当前按钮指向ring的i位置的字符，要去解决key中第j位置的字符  
         public static int[][]dp=new int[MAXN][MAXN];  
   
         //初始化函数  
         public static void build(String ring, String key){  
             char[]rin=ring.toCharArray();  
             n=rin.length;  
             char[]ke=key.toCharArray();  
             m=ke.length;  
             Arrays.fill(size,0);  
             //接下来将ring中的字符全部转化放入rings,size,where中  
             for(int i=0,v;i<n;i++){  
                 v=rin[i]-'a';  
                 rings[i]=v;  
                 where[v][size[v]++]=i;  
             }  
   
             //将key中的字符转化到keys中去  
             for(int j=0,v;j<m;j++){  
                 v=ke[j]-'a';  
                 keys[j]=v;  
             }  
   
             for(int i=0;i<n;i++){  
                 for(int j=0;j<m;j++){  
                     dp[i][j]=-1;  
                 }  
             }  
         }  
   
         public static int findRotateSteps(String ring, String key) {  
             build(ring,key);  
             return f(0,0);  
         }  
   
   
         public static int f(int i,int j){  
             if(j==m){  
                 // key长度是m  
                 // 都搞定  
                 return 0;  
             }  
             if(dp[i][j]!=-1){  
                 return dp[i][j];  
             }  
             int ans=0;  
             if(rings[i]==keys[j]){  
                 ans=f(i,j+1)+1;  
             }else{  
                 //顺时针找到最近位置  
                 int u=clock(i,j);  
                 int distance1=(u>i?(u-i):(n-i+u));  
                 //逆时针找到最近位置  
                 int v=counterClock(i,j);  
                 int distance2=(v<i?(i-v):(n-v+i));  
                 ans=Math.min(f(u,j)+distance1,f(v,j)+distance2);  
             }  
             dp[i][j]=ans;  
             return ans;  
         }  
   
   
         //顺时针找到离ring字符中i位置与key字符中j位置的字符相等的最近位置  
         public static int clock(int i,int j){  
             //j字符为  
             int v=keys[j];  
             int l=0;  
             int r=size[v]-1;  
             int ans=0;  
             int m;  
             while(l<=r){  
                 m=(l+r)/2;  
                 if(where[v][m]>i){  
                     r=m-1;  
                     ans=m;  
                 }else{  
                     l=m+1;  
                 }  
             }  
             return where[v][ans];  
         }  
   
         //逆时针找到离ring字符中i位置与key字符中j位置的字符相等的最近位置  
         public static int counterClock(int i,int j){  
             //j字符为  
             int v=keys[j];  
             int l=0;  
             int r=size[v]-1;  
             int ans=r;  
             int m;  
             while(l<=r){  
                 m=(l+r)/2;  
                 if(where[v][m]<i){  
                     l=m+1;  
                     ans=m;  
                 }else{  
                     r=m-1;  
                 }  
             }  
             return where[v][ans];  
         }  
   
     }  
 }

4、累加和不大于k的最长子数组

题目描述：给定一个无序数组arr，其中元素可正、可负、可0。给定一个整数k，求arr所有的子数组中累加和小于或等于k的最长子数组长度

例如：arr = [3, -2, -4, 0, 6], k = -2. 相加和小于等于-2的最长子数组为{3, -2, -4, 0}，所以结果返回4

[要求] 时间复杂度为O(n)O(n)，空间复杂度为O(n)O(n) 输入描述：

第一行两个整数N, k。N表示数组长度，k的定义已在题目描述中给出第二行N个整数表示数组内的数输出描述：

输出一个整数表示答案示例1

输入：

5 -2 3 -2 -4 0 6

输出：

4 备注： 1⩽N⩽1051⩽N⩽105 −109⩽k⩽109−109⩽k⩽109 −100⩽arri⩽100−100⩽arri⩽100

解题思路：

解法一：最大前缀和解法O (nlogn)
- 依次求出数组的每个位置的最大前缀和
- 然后计算每个位置的前缀和，对每个位置用二分查找，寻找当前位置往前最左的>=前缀和sum-k的位置
- 计算差值，取最大的那个
- 但是我最开始写的时候直接就用前缀和+二分查找来做，没有求最大前缀和数组，忘记了二分查找只能在数组有序的时候使用。
解法二：最小前缀和+滑动窗口的解法O (n)
- 求解以每个位置作为起始位置的最小前缀和以及其结尾位置（这会形成以某个位置开始的最小前缀和窗口）
- 既然要求前缀和<=k, 那么我们就从头判断每个数字开始的最小前缀和窗口是否小于=k，是的话就尝试加上下一个最小前缀和窗口，一直到最小前缀和窗口和>k的位置停住
- 拿到我们可以拿到的最大窗口，计算窗口大小，取最大的那个
- 减去当前窗口最左边的值，窗口开始缩小，然后再尝试加上后面的最小前缀和窗口
- 这个最优解中包含的贪心思想（窗口的加速建立、可能性的淘汰），是这个题的重点

代码如下

 package main.java.class083;  
 import java.io.*;  
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code04_LongestSubarraySumNoMoreK  
  * @description: 累加和不大于k的最长子数组  
  * // 给定一个无序数组arr，长度为n，其中元素可能是正、负、0  
  * // 给定一个整数k，求arr所有的子数组中累加和不大于k的最长子数组长度  
  * // 要求时间复杂度为O(n)  
  * // 测试链接 : https://www.nowcoder.com/practice/3473e545d6924077a4f7cbc850408ade  
  * @author: zs宝  
  * @create: 2025-10-08 11:33  
  * @Version 1.0  
  **/public class Code04_LongestSubarraySumNoMoreK {  
     // 注意类名必须为 Main, 不要有任何 package xxx 信息  
     public class Main {  
         public static int MAXN = 100001;  
         public static int[]nums = new int[MAXN];  
         public static int n, k;  
         //minSums[i]以当前i元素为起点，可以得到的最小前缀和是多少  
         public static int[] minSums=new int[MAXN];  
         //minSumEnds[i]:minSums[i]以当前i元素为起点，可以得到的最小前缀和的终点位置  
         public static int[] minSumEnds=new int[MAXN];  
         public static void main(String[] args) throws IOException {  
             BufferedReader buffer = new BufferedReader(new InputStreamReader(System.in));  
             StreamTokenizer in = new StreamTokenizer(buffer);  
             PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));  
             while (in.nextToken() != StreamTokenizer.TT_EOF) {  
                 n = (int)in.nval;  
                 in.nextToken();  
                 k = (int)in.nval;  
                 for (int i = 0; i < n; i++) {  
                     in.nextToken();  
                     nums[i] = (int)in.nval;  
                 }  
                 out.println(compute2());  
             }  
             out.flush();  
             out.close();  
             buffer.close();  
         }  
   
         //前缀和的解法，时间复杂度O(nlogn)  
         public static int compute1(){  
             int[]sums=new int[n+1];  
             int ans=0;  
             for(int i=0,sum=0;i<n;i++){  
                 sum+=nums[i];  
                 //维护一个最大前缀合的有序数组  
                 sums[i+1]=Math.max(sums[i],sum);  
             }  
             //开始二分查找寻找每个位置作为结尾的符合要求的最左位置  
             for(int i=0,sum=0,pre;i<n;i++){  
                 sum+=nums[i];  
                 pre=find(sums,sum-k,i+1);  
                 //sums中对应的pre位置，在nums数组应该为pre-1  
                 ans=Math.max(ans,i-pre+1);  
             }  
             return ans;  
         }  
   
         public static int find(int[]sums,int sum,int i){  
             int l=0;  
             int r=i;  
             int m;  
             int ans=-1;  
             while(l<=r){  
                 m=(l+r)/2;  
                 if(sums[m]>=sum){  
                     r=m-1;  
                     ans=m;  
                 }else{  
                     l=m+1;  
                 }  
             }  
             return ans==-1?i:ans;  
         }  
   
         //最小前缀和+滑动窗口加速，做到时间复杂度O(N)  
         public static int compute2(){  
             //初始化minSums，minSumEnds数组  
             minSums[n-1]=nums[n-1];  
             minSumEnds[n-1]=n-1;  
             for(int i=n-2;i>=0;i--){  
                 //最小  
                 if(minSums[i+1]<=0){  
                     minSums[i]=nums[i]+minSums[i+1];  
                     minSumEnds[i]=minSumEnds[i+1];  
                 }else{  
                     minSums[i]=nums[i];  
                     minSumEnds[i]=i;  
                 }  
             }  
             int ans=0;  
             //开始滑动窗口遍历加速，找到最大窗口  
             for(int i=0,end=0,sum=0;i<n;i++){  
                 //先找到一段窗口，其窗口内的值和<=k  
                 while(end<n && sum+minSums[end]<=k){  
                     sum=sum+minSums[end];  
                     end=minSumEnds[end]+1;  
                 }  
                 if(end>i){  
                     // 如果end > i，  
                     // 窗口范围：i...end-1，那么窗口有效  
                     ans=Math.max(ans,end-i);  
                     sum-=nums[i];  
                 }else{  
                     // 如果end == i，那么说明窗口根本没扩出来，代表窗口无效  
                     // end来到i+1位置，然后i++了  
                     // 继续以新的i位置做开头去扩窗口  
                     end++;  
                 }  
             }  
             return ans;  
         }  
     }  
 }

参考资料

左程云-算法通关系列-083

如果觉得文章对你有用，请随意赞赏

算法动态规划

动态规划18：用观察法优化枚举-下

https://zshunbao.top/archives/dong-tai-gui-hua-18-yong-guan-cha-fa-you-hua-mei-ju-xia

作者

zs宝

发布于

2025-10-08

更新于

2025-10-08

许可协议

CC BY 4.0