核心思想
狭义的贪心 每一步都做出在当前状态下最好或最优的选择,从而希望最终的结果是最好或最优的算法
广义的贪心 通过分析题目自身的特点和性质,只要发现让求解答案的过程得到加速的结论,都算广义的贪心
贪心是最符合自然智慧的思想,一般分析门槛不高 理解基本的排序、有序结构,有基本的逻辑思维就能理解 但是贪心的题目,千题千面,极难把握 难度在于证明局部最优可以得到全局最优,好在!我们有对数器!贪心专题2、3,这两节大量使用对数器
有关贪心的若干现实 & 提醒
1、不要去纠结严格证明,每个题都去追求严格证明,浪费时间、收益很低,而且千题千面。玄学!
2、一定要掌握用对数器验证的技巧,这是解决贪心问题的关键
3、解法几乎只包含贪心思路的题目,代码量都不大
4、大量累积贪心的经验,重点不是证明,而是题目的特征,以及贪心方式的特征,做好总结方便借鉴
5、关注题目数据量,题目的解可能来自贪心,也很可能不是,如果数据量允许,能不用贪心就不用(稳)
6、贪心在笔试中出现概率不低,但是面试中出现概率较低,原因是 淘汰率 vs 区分度
7、广义的贪心无所不在,可能和别的思路结合,一般都可以通过自然智慧想明白,依然不纠结证明
本章节还有一个特别重要的小知识点,乘法快速幂 假设我们需要求解 10^75, 如果我们直接用75个10相乘结果太慢, 且乘的次数太多,且当幂太大时容易超出最大的数值范围 而这里就有一种专门的快速幂的方式来解决这个问题,快速幂就是:
利用指数的二进制表示,把指数 n 拆成若干个 2 的幂次之和,从而把幂运算变成若干次平方和乘法的组合。 例如:a13=a1101=a8×a4×a^1 这里75=1001011,那么1075=101* 10^2 * 10^8 * 10^64, 将75次的乘法运算,变成了log75次的乘法组合
模版代码如下
// 快速幂,求余数
// 求x的n次方,最终得到的结果 % mod
public static long power(long x, int n, int mod) {
long ans = 1;
while (n > 0) {
if ((n & 1) == 1) {
//若当前位为1
ans = (ans * x) % mod;
}
//由于指数转为了二进制,每一高位上的数值都为低位上的2倍,反应在具体数值上就是2^8==2^4 * 2^4这种
x = (x * x) % mod;
n >>= 1;
}
return ans;
}
例题
1、[砍竹子Ⅱ](https://leetcode.cn/problems/jian-sheng-zi-ii-lcof/
) 题目描述:
现需要将一根长为正整数 bamboo_len 的竹子砍为若干段,每段长度均为 正整数。请返回每段竹子长度的 最大乘积 是多少。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:bamboo_len = 12 输出:81
提示:
2 <= bamboo_len <= 1000
注意:本题与主站 343 题相同: https://leetcode-cn.com/problems/integer-break/
解题思路:
观察数值的最优解的规律
最后用规律结合快速幂进行贪心
代码如下
package main.java.class090;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code01_CuttingBamboo
* @description: 砍竹子II
* // 现需要将一根长为正整数bamboo_len的竹子砍为若干段
* // 每段长度均为正整数
* // 请返回每段竹子长度的最大乘积是多少
* // 答案需要对 1000000007 取模
* // 测试链接 : https://leetcode.cn/problems/jian-sheng-zi-ii-lcof/
* @author: zs宝
* @create: 2025-10-23 09:01
* @Version 1.0
**/public class Code01_CuttingBamboo {
class Solution {
public int cuttingBamboo(int x) {
if(x==2){
return 1;
}
if(x==3){
return 2;
}
int mod=1000000007;
// n = 4 -> 2 * 2
// n = 5 -> 3 * 2 // n = 6 -> 3 * 3 // n = 7 -> 3 * 2 * 2 // n = 8 -> 3 * 3 * 2 // n = 9 -> 3 * 3 * 3 // n = 10 -> 3 * 3 * 2 * 2 // n = 11 -> 3 * 3 * 3 * 2 // n = 12 -> 3 * 3 * 3 * 3 //根据观察规律
int tail=x%3==0?1:(x%3==1?4:2);
//求解有几个3相乘
int n=(tail==1?x:(x-tail))/3;
return (int)((power(3,n,mod)*tail)%mod);
}
//快速幂
//x^n
public long power(long x,int n,int mod){
long ans=1;
while(n>0){
if((n&1)==1){
ans=(ans*x)%mod;
}
x=(x*x)%mod;
n>>=1;
}
return ans;
}
}
}2、分成k份的最大乘积
题目描述: 一个数字n一定要分成k份,得到的乘积尽量大是多少 数字n和k,可能非常大,到达10^12规模 结果可能更大,所以返回结果对1000000007取模 来自真实大厂笔试,没有在线测试,对数器验证
解题思路:
这个题的思路其实一个中学常见的数学规律,一个数字分为K份的乘积最大,是在这K份的数字尽量相同时
代码如下
package main.java.class090;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code02_MaximumProduct
* @description: 分成k份的最大乘积
* // 一个数字n一定要分成k份,得到的乘积尽量大是多少
* // 数字n和k,可能非常大,到达10^12规模
* // 结果可能更大,所以返回结果对 1000000007 取模
* // 来自真实大厂笔试,没有在线测试,对数器验证
* @author: zs宝
* @create: 2025-10-23 09:38
* @Version 1.0
**/public class Code02_MaximumProduct {
// 贪心的解
// 这是最优解
// 如果结果很大,那么求余数
public static int maxValue2(int n, int k) {
int mod = 1000000007;
long a=n/k;
int b=n%k;
long ans1=power(a+1,b,mod);
long ans2=power(a,k-b,mod);
return (int)((ans2*ans1)%mod);
}
//快速幂
//x^n
public static long power(long x,int n,int mod){
long ans=1;
while(n>0){
if((n&1)==1){
ans=(ans*x)%mod;
}
x=(x*x)%mod;
n>>=1;
}
return ans;
}
// 暴力递归
// 为了验证
public static int maxValue1(int n, int k) {
return f1(n, k);
}
// 剩余的数字rest拆成k份
// 返回最大乘积
// 暴力尝试一定能得到最优解
public static int f1(int rest, int k) {
if (k == 1) {
return rest;
}
int ans = Integer.MIN_VALUE;
for (int cur = 1; cur <= rest && (rest - cur) >= (k - 1); cur++) {
int curAns = cur * f1(rest - cur, k - 1);
ans = Math.max(ans, curAns);
}
return ans;
}
// 对数器
// 为了验证
public static void main(String[] args) {
int N = 30;
int testTimes = 2000;
System.out.println("测试开始");
for (int i = 1; i <= testTimes; i++) {
int n = (int) (Math.random() * N) + 1;
int k = (int) (Math.random() * n) + 1;
int ans1 = maxValue1(n, k);
int ans2 = maxValue2(n, k);
if (ans1 != ans2) {
// 如果出错了
// 可以增加打印行为找到一组出错的例子
// 然后去debug
System.out.println("出错了!");
}
if (i % 100 == 0) {
System.out.println("测试到第" + i + "组");
}
}
System.out.println("测试结束");
}
}3、会议必须独占时间段的最大会议数量
题目描述: 给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
注意 只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。 提示:
1 <= intervals.length <= 105intervals[i].length == 2-5 * 104 <= starti < endi <= 5 * 104
解题思路:
这个题的要求是求出需要移除区间的最小数量,使剩余区间互不重叠。那么就可以转化为总数量-互不重叠的区间的最大数量。
问题就转化为了求解互不重叠区间的最大数量
我们之前求解过区间内重叠区间的最大数量,例如 089、贪心经典题目专题1 的第四题,这个题的解法是先将数组按照开始时间排序,然后依次遍历区间,如果当前区间的开始时间小于小根堆(越小,两个区间重叠的概率越大)堆顶元素(存储的是区间终止位置),就将当前区间的终止位置加入小根堆,堆的size最大值就是重叠区间的最大数量
现在我们要求解互不重叠区间的最大数量,我们的贪心策略
按照区间的结束位置排序(越早结束的,大区间内互不重叠的小区间数量就大概率越多)
一次遍历数组,每次遍历时,两个区间不重叠时,数量加加,当前时间改为当前数组的结束时间
代码如下
package main.java.class090;
import java.util.Arrays;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code03_MeetingMonopoly1
* @description: 会议必须独占时间段的最大会议数量
* // 给定若干会议的开始、结束时间
* // 你参加某个会议的期间,不能参加其他会议
* // 返回你能参加的最大会议数量
* // 同学找到了Leetcode的在线测试,题意类似
* // 测试链接 :https://leetcode.cn/problems/non-overlapping-intervals/
* @author: zs宝
* @create: 2025-10-23 09:47
* @Version 1.0
**/public class Code03_MeetingMonopoly1 {
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
int n=intervals.length;
Arrays.sort(intervals,(a, b)->a[1]-b[1]);
int cur=-50001;
//求出最多可以参加几个会议
int ans=0;
for(int i=0;i<n;i++){
if(cur<=intervals[i][0]){
ans++;
cur=intervals[i][1];
}
}
return n-ans;
}
}
}4、会议只占一天的最大会议数量
题目描述: 给你一个数组 events,其中 events[i] = [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。
你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。在任意一天 d 中只能参加一场会议。
请你返回你可以参加的 最大 会议数目。
示例 1:
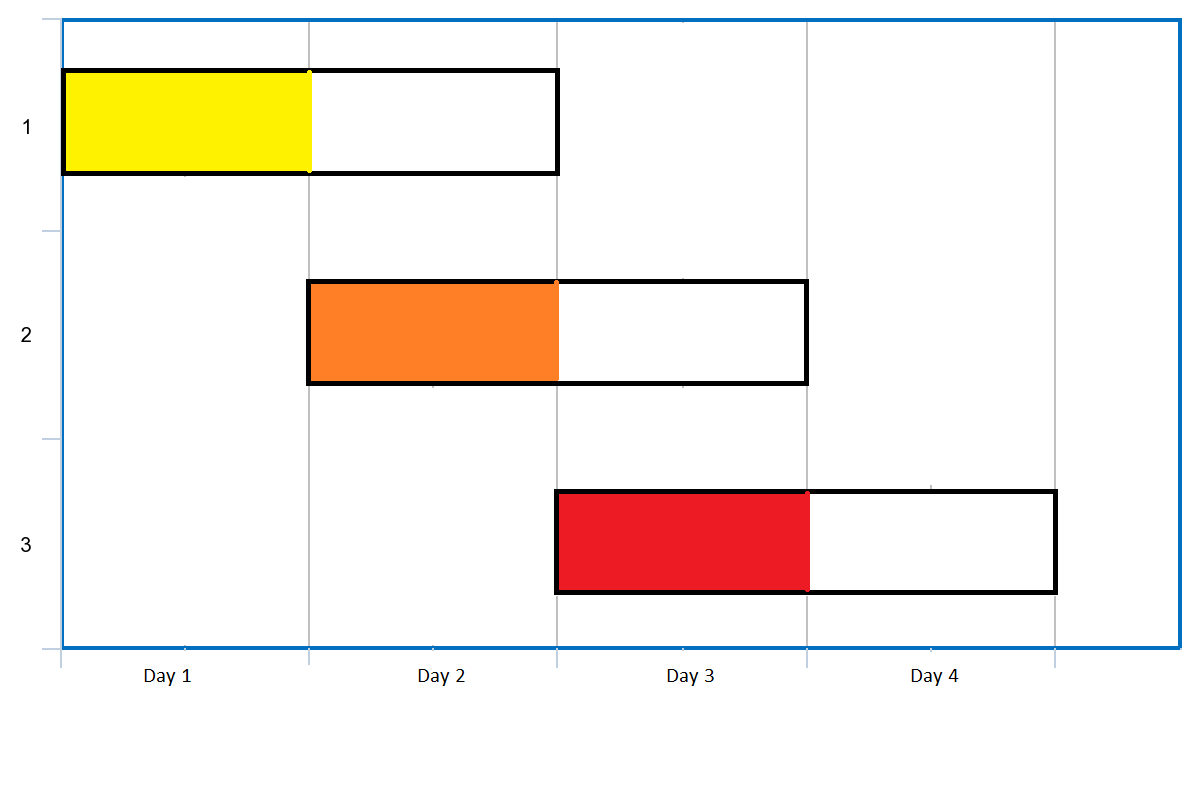
输入:events = [[1,2],[2,3],[3,4]] 输出:3 解释:你可以参加所有的三个会议。 安排会议的一种方案如上图。 第 1 天参加第一个会议。 第 2 天参加第二个会议。 第 3 天参加第三个会议。
示例 2:
输入:events= [[1,2],[2,3],[3,4],[1,2]] 输出:4
提示:
1 <= events.length <= 105events[i].length == 21 <= startDayi <= endDayi <= 105
解题思路:
这个题同样是会议室的哪一类,但是贪心的策略根上一题并不一样。原因是代价不同了,上一题的代价是真个区间段都必须待在那一个区间,这个是只用待区间的一天即可
贪心策略如下
先将数组按照开始时间排序,然后建立一个小根堆,小根堆存放会议的结束时间,越早结束越紧迫。由于只需要待一天,那种越早结束的去一天也就越能留出后续时间参加更多的会议
遍历时,将当前时间开始的会议加入小根堆,弹出已经过期的会议
从还剩的会议中,徐州呢一个最紧迫的去参加,即小根堆堆顶
代码如下
package main.java.class090;
import java.util.Arrays;
import java.util.PriorityQueue;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code04_MeetingOneDay
* @description: 会议只占一天的最大会议数量
* // 给定若干会议的开始、结束时间
* // 任何会议的召开期间,你只需要抽出1天来参加
* // 但是你安排的那一天,只能参加这个会议,不能同时参加其他会议
* // 返回你能参加的最大会议数量
* // 测试链接 : https://leetcode.cn/problems/maximum-number-of-events-that-can-be-attended/
* @author: zs宝
* @create: 2025-10-23 10:26
* @Version 1.0
**/public class Code04_MeetingOneDay {
class Solution {
public int maxEvents(int[][] events) {
Arrays.sort(events,(a, b)->a[0]-b[0]);
int n=events.length;
//找到所有会议最早的开始时间,最晚的结束时间
int min=events[0][0];
int max=events[0][1];
for(int i=1;i<n;i++){
max=Math.max(max,events[i][1]);
}
int ans=0;
//用一个小根堆存储会议结束时间,越早结束,越紧迫
PriorityQueue<Integer> heap=new PriorityQueue<>();
for(int day=min,i=0;day<=max;day++){
//来到这一天先把,这一天开始的会议全部加入小根堆,代表这些会议可以参加了
while(i<n && day==events[i][0]){
heap.add(events[i++][1]);
}
//将当前小根堆中存储的已经过期的会议排除
while(!heap.isEmpty() && heap.peek()<day){
heap.poll();
}
//从小根堆弹出一个最紧迫的会议,去参加
if(!heap.isEmpty() && day<=heap.peek()){
ans++;
heap.poll();
}
}
return ans;
}
}
}5、IPO
题目描述: 假设 力扣(LeetCode)即将开始 IPO 。为了以更高的价格将股票卖给风险投资公司,力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限,它只能在 IPO 之前完成最多 k 个不同的项目。帮助 力扣 设计完成最多 k 个不同项目后得到最大总资本的方式。
给你 n 个项目。对于每个项目 i ,它都有一个纯利润 profits[i] ,和启动该项目需要的最小资本 capital[i] 。
最初,你的资本为 w 。当你完成一个项目时,你将获得纯利润,且利润将被添加到你的总资本中。
总而言之,从给定项目中选择 最多 k 个不同项目的列表,以 最大化最终资本 ,并输出最终可获得的最多资本。
答案保证在 32 位有符号整数范围内。
示例 1:
输入:k = 2, w = 0, profits = [1,2,3], capital = [0,1,1] 输出:4 解释: 由于你的初始资本为 0,你仅可以从 0 号项目开始。 在完成后,你将获得 1 的利润,你的总资本将变为 1。 此时你可以选择开始 1 号或 2 号项目。 由于你最多可以选择两个项目,所以你需要完成 2 号项目以获得最大的资本。 因此,输出最后最大化的资本,为 0 + 1 + 3 = 4。
示例 2:
输入:k = 3, w = 0, profits = [1,2,3], capital = [0,1,2] 输出:6
提示:
1 <= k <= 1050 <= w <= 109n == profits.lengthn == capital.length1 <= n <= 1050 <= profits[i] <= 1040 <= capital[i] <= 109
解题思路:
要获得最大资产
先按照项目所需要的资本将数组排序
将当前拥有资产可以投资的项目加入大根堆中,大根堆存放投资后的纯利润
当前资产加上大根堆的项目中的利润最大的那个
做K次这种行为
代码如下:
package main.java.class090;
import java.util.Arrays;
import java.util.PriorityQueue;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code05_IPO
* @description: IPO
* // 给你n个项目,对于每个项目i
* // 它都有一个纯利润profits[i]
* // 和启动该项目需要的最小资本capital[i]
* // 最初你的资本为w,当你完成一个项目时,你将获得纯利润,添加到你的总资本中
* // 总而言之,从给定项目中选择最多k个不同项目的列表
* // 以最大化最终资本,并输出最终可获得的最多资本
* // 测试链接 : https://leetcode.cn/problems/ipo/
* @author: zs宝
* @create: 2025-10-23 10:56
* @Version 1.0
**/public class Code05_IPO {
class Solution {
public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
int n=profits.length;
//用来存储每一个项目的纯收益和需要的资本
int[][]costs=new int[n][2];
for(int i=0;i<n;i++){
costs[i][0]=profits[i];
costs[i][1]=capital[i];
}
//根据投资需要的最小资本排序
Arrays.sort(costs,(a, b)->a[1]-b[1]);
//创建一个大根堆,存储每个项目的纯利润
PriorityQueue<Integer> heap=new PriorityQueue<>((a, b)->b-a);
for(int i=0,j=0;i<k;i++){
//将当前资产量可以投资的项目加载进小根堆
while(j<n && costs[j][1]<=w){
heap.add(costs[j++][0]);
}
//选取一个利润最大的投资
if(!heap.isEmpty()){
w+=heap.poll();
}
}
return w;
}
}
}6、加入差值绝对值直到长度固定
题目描述: 给定一个非负数组arr,计算任何两个数差值的绝对值 如果arr中没有,都要加入到arr里,但是只加一份 然后新的arr,继续计算任何两个数差值的绝对值 如果arr中没有,都要加入到arr里,但是只加一份 一直到arr大小固定,返回arr最终的长度 来自真实大厂笔试,没有在线测试,对数器验证
解题思路:
这是一个数学规律
找到数组内的最大公因数
那么最终至少有数组最大值/最大公因数个数
最后看数组内是否有重复值,加上原有的重复个数
最后判断0的个数
代码如下
package main.java.class090;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
/**
* @program: ZuoChengxunAlgorithmClass
* @ClassName Code06_AbsoluteValueAddToArray
* @description: 加入差值绝对值直到长度固定
* // 给定一个非负数组arr,计算任何两个数差值的绝对值
* // 如果arr中没有,都要加入到arr里,但是只加一份
* // 然后新的arr继续计算任何两个数差值的绝对值,
* // 如果arr中没有,都要加入到arr里,但是只加一份
* // 一直到arr大小固定,返回arr最终的长度
* // 来自真实大厂笔试,没有在线测试,对数器验证
* @author: zs宝
* @create: 2025-10-23 11:09
* @Version 1.0
**/public class Code06_AbsoluteValueAddToArray {
//求解两数的最大公约数
public static int gcd(int m, int n) {
return n == 0 ? m : gcd(n, m % n);
}
// 正式方法
// 时间复杂度O(n)
public static int len2(int[] arr) {
int max=0;
//找到任意一个不为0的数
int gcd=0;
for(int num:arr){
if(num!=0){
gcd=num;
}
max=Math.max(num,max);
}
//没有一个非0的数
if(gcd==0){
return arr.length;
}
//统计每个数出现的次数
HashMap<Integer,Integer> cnts=new HashMap<>();
for(int num:arr){
//寻找数组内,所有数值的最大公约数
if(num!=0){
gcd=gcd(gcd,num);
}
cnts.put(num,cnts.getOrDefault(num,0)+1);
}
//最终数组至少应该有这么多个数
int ans=max/gcd;
//寻找原数组内相同数值出现的最大次数
int maxCnt=0;
//看看原数组中有没有重复的数值
for(int key: cnts.keySet()){
if(key!=0){
ans+=cnts.get(key)-1;
}
maxCnt=Math.max(maxCnt,cnts.get(key));
}
//判断0这个数值
ans+=cnts.getOrDefault(0,maxCnt>1?1:0);
return ans;
}
// 暴力方法
// 为了验证
public static int len1(int[] arr) {
ArrayList<Integer> list = new ArrayList<>();
HashSet<Integer> set = new HashSet<>();
for (int num : arr) {
list.add(num);
set.add(num);
}
while (!finish(list, set))
;
return list.size();
}
public static boolean finish(ArrayList<Integer> list, HashSet<Integer> set) {
int len = list.size();
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
int abs = Math.abs(list.get(i) - list.get(j));
if (!set.contains(abs)) {
list.add(abs);
set.add(abs);
}
}
}
return len == list.size();
}
// 为了测试
public static int[] randomArray(int n, int v) {
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[i] = (int) (Math.random() * v);
}
return ans;
}
// 为了测试
public static void main(String[] args) {
int N = 50;
int V = 100;
int testTimes = 20000;
System.out.println("测试开始");
for (int i = 0; i < testTimes; i++) {
int n = (int) (Math.random() * N) + 1;
int[] nums = randomArray(n, V);
int ans1 = len1(nums);
int ans2 = len2(nums);
if (ans1 != ans2) {
System.out.println("出错了!");
}
}
System.out.println("测试结束");
}
}