前置知识: 讲解054 - 单调队列讲解067、讲解068 - 二维动态规划及其空间压缩技巧讲解073 - 01背包讲解074 - 完全背包【必备】课程的动态规划大专题从讲解066开始，建议从头开始学习会比较系统

核心思想

多重背包：每一种物品给定数量的限制，进行可能性展开多重背包的枚举优化：二进制分组优化（最常用）、单调队列优化（复杂度最好，理解稍难）

混合背包：多种背包模型的组合与转化

例题

1、宝物筛选 -多重背包不进行枚举优化

题目描述：一共有n种货物, 背包容量为t 每种货物的价值 (v[i])、重量 (w[i])、数量 (c[i]) 都给出请返回选择货物不超过背包容量的情况下，能得到的最大的价值

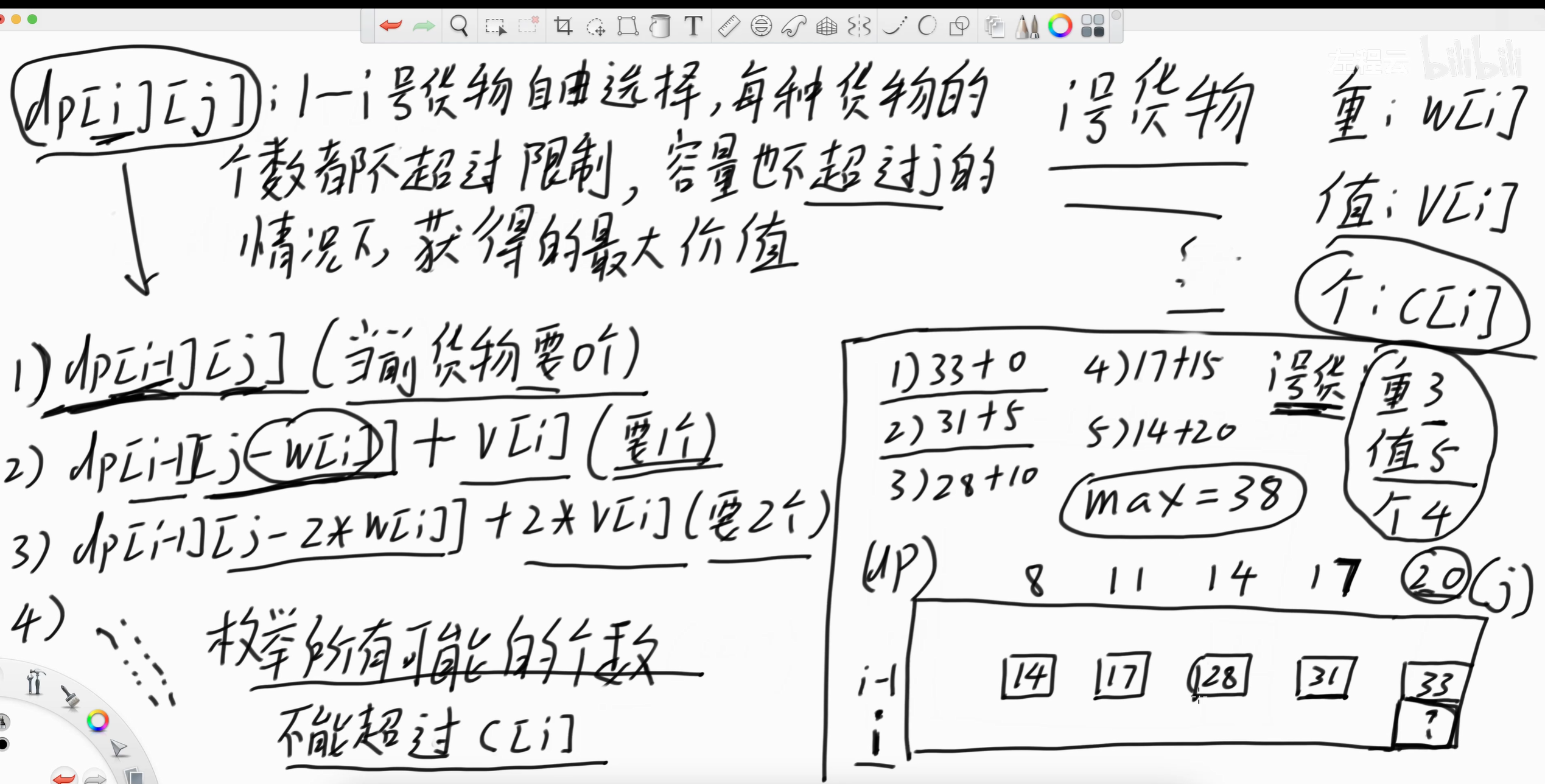
解题思路：

这是多重背包的一个基础模版
最基本的解法就是再01背包要的时候，不再只要1次，而是根据物品数量和背包容量多要多次
其余与01背包几乎一致
注意：这个解法过不了本题，会超时

代码如下

 package main.java.class075;  
   
 import java.io.*;  
 import java.util.Arrays;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code01_BoundedKnapsack  
  * @description: 多重背包不进行枚举优化  
  * // 宝物筛选  
  * // 一共有n种货物, 背包容量为t  
  * // 每种货物的价值(v[i])、重量(w[i])、数量(c[i])都给出  
  * // 请返回选择货物不超过背包容量的情况下，能得到的最大的价值  
  * // 测试链接 : https://www.luogu.com.cn/problem/P1776  
  * @author: zs宝  
  * @create: 2025-09-09 09:35  
  * @Version 1.0  
  **/public class Code01_BoundedKnapsack {  
     public static int MAXW=40001;  
     public static int MAXN=101;  
     public static int n,w;  
     public static int[] val=new int[MAXN];  
     public static int[] weight=new int[MAXN];  
     public static int[] cnts=new int[MAXN];  
     public static int[]dp=new int[MAXW];  
   
     public static void main(String[] args) throws IOException {  
         BufferedReader buffer=new BufferedReader(new InputStreamReader(System.in));  
         StreamTokenizer in=new StreamTokenizer(buffer);  
         PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));  
         while (in.nextToken()!=StreamTokenizer.TT_EOF){  
             n=(int)in.nval;  
             in.nextToken();  
             w=(int)in.nval;  
             for(int i=1;i<=n;i++){  
                 in.nextToken();  
                 val[i]=(int)in.nval;  
                 in.nextToken();  
                 weight[i]=(int)in.nval;  
                 in.nextToken();  
                 cnts[i]=(int)in.nval;  
             }  
             out.println(compute1());  
         }  
         out.flush();  
         out.close();  
         buffer.close();  
     }  
   
     //严格依赖位置的动态规划  
     //时间复杂度O(n * t * 每种商品的平均个数)  
     public static int compute1(){  
         // dp[0][....] = 0，表示没有货物的情况下，背包容量不管是多少，最大价值都是0  
         int[][]dp=new int[n+1][w+1];  
         for(int i=1;i<=n;i++){  
             for(int j=0;j<=w;j++){  
                 dp[i][j]=dp[i-1][j];  
                 for(int k=1;k<=cnts[i] && weight[i]*k<=j;k++){  
                     dp[i][j]=Math.max(dp[i][j],dp[i-1][j-weight[i]*k]+k*val[i]);  
                 }  
             }  
         }  
         return dp[n][w];  
     }  
   
     //严格依赖位置的动态规划+空间压缩  
     public static int compute2(){  
         Arrays.fill(dp,0,n+1,0);  
         for(int i=1;i<=n;i++){  
             for(int j=w;j>=0;j--){  
                 for(int k=1;k<=cnts[i] && weight[i]*k<=j;k++){  
                     dp[j]=Math.max(dp[j],dp[j-weight[i]*k]+k*val[i]);  
                 }  
             }  
         }  
         return dp[w];  
     }  
 }

2、宝物筛选 -二进制分组转化优化(模版)、

解题思路

这个题就是第一个题，但是上一个题使用的多重背包最基础的解法，很多时候无法通过
究其原因是因为多重背包基础的3个for循环，如何进行优化它呢？
这里关于多重背包的解法，使用二进制分组转化成01背包进行优化。
我们在上面一题的解法中说过，除了在01背包要的时候，不再只要1次，而是根据物品数量和背包容量多要多次，多重背包的基础解法几乎与01背包一致
那么能不能将多重背包就转为01背包呢？如何转
多重背包在题意上与01背包的唯一区别就是物品数量多，每次要的时候可以要多个，而01背包只要能要1个，而多重背包的第三层for循环也是因此而来，那么我们可不可以将每个物品的不同数量也当成一个新物品，如物品a, 有3个，那么我们分别将1个a, 2个a, 3个a分别当作一个物品，将其加入物品列表。
但是上述修改，随便可以根据01背包来做，没了第三层循环，但是物品量的增加第一层循环增加巨大，实际的时间复杂度相比基础解法几乎一致。
我们能不能用上面思想的同时，减少第一层循环增加的物品量，但是要做到能够通过新增的物品通过组合覆盖掉多重背包物品的所有可能。
这里就有了二进制分组转化。假设原本a物品的数量为18,1<18, 那么可以有1个a组成的新物品，18-1=17，然后2^1<17, 于是有由2个a组成的新物品，17-2=15，然后2^2<15, 于是有4个a组成的新物品，15-4=11，然后2^3<11, 于是有8个a组成的新物品，11-8=3, 如何2^4=16>11, 于是最终还剩下的3个a组成一个新物品。
所以原本的18个a分组为：1,2,4,8,3。而18种剩下的如5,6,11等其它数字都可以由这几个分组组合出来。
于是原本的多重背包解法得以优化。

代码如下

 package main.java.class075;  
   
 import java.io.*;  
 import java.util.Arrays;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code02_BoundedKnapsackWithBinarySplitting  
  * @description: 多重背包通过二进制分组转化成01背包(模版)  
  * // 宝物筛选  
  * // 一共有n种货物, 背包容量为t  
  * // 每种货物的价值(v[i])、重量(w[i])、数量(c[i])都给出  
  * // 请返回选择货物不超过背包容量的情况下，能得到的最大的价值  
  * // 测试链接 : https://www.luogu.com.cn/problem/P1776  
  * @author: zs宝  
  * @create: 2025-09-09 10:05  
  * @Version 1.0  
  **/public class Code02_BoundedKnapsackWithBinarySplitting {  
     public static int MAXW = 40001;  
     public static int MAXN=1001;  
     public static int n, w, m;  
     public static int[] val = new int[MAXN];  
     public static int[] weights = new int[MAXN];  
     public static int[] cnts = new int[MAXN];  
     public static int[] dp = new int[MAXW];  
   
     public static void main(String[] args) throws IOException {  
         BufferedReader buffer = new BufferedReader(new InputStreamReader(System.in));  
         StreamTokenizer in = new StreamTokenizer(buffer);  
         PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));  
         while (in.nextToken() != StreamTokenizer.TT_EOF) {  
             n = (int) in.nval;  
             in.nextToken();  
             w = (int) in.nval;  
             m = 0;  
             for (int i = 1, value, weight, cnt; i <= n; i++) {  
                 in.nextToken();  
                 value = (int) in.nval;  
                 in.nextToken();  
                 weight = (int) in.nval;  
                 in.nextToken();  
                 cnt = (int) in.nval;  
   
                 //接下来这段代码是最重要的优化  
                 //进行二进制分组优化  
                 // 一般都使用这种技巧，这段代码非常重要  
                 // 虽然时间复杂度不如单调队列优化的版本  
                 // 但是好写，而且即便是比赛，时间复杂度也达标  
                 // 二进制分组的时间复杂度为O(log cnt)  
                 for (int k = 1; k <= cnt; k <<= 1) {  
                     val[++m] = value * k;  
                     weights[m] = weight * k;  
                     cnt -= k;  
                 }  
                 if (cnt > 0) {  
                     val[++m] = value * cnt;  
                     weights[m] = weight * cnt;  
                 }  
             }  
             out.println(compute());  
         }  
         out.flush();  
         out.close();  
         buffer.close();  
     }  
   
     //01背包的严格以来位置的动态规划+空间压缩  
     public static int compute() {  
         Arrays.fill(dp, 0, w + 1, 0);  
         for (int i = 1; i <= m; i++) {  
             for (int j = w; j >= weights[i]; j--) {  
                 dp[j] = Math.max(dp[j], dp[j - weights[i]] + val[i]);  
             }  
         }  
         return dp[w];  
     }  
 }

3、观赏樱花

题目描述：给定一个背包的容量t，一共有n种货物，并且给定每种货物的信息花费 (cost)、价值 (val)、数量 (cnt) 如果cnt == 0，代表这种货物可以无限选择如果cnt > 0，那么cnt代表这种货物的数量挑选货物的总容量在不超过t的情况下，返回能得到的最大价值背包容量不超过1000，每一种货物的花费都>0

解题思路：

这就是一个非常典型的多重背包问题

代码如下

 package main.java.class075;  
   
 import java.io.*;  
 import java.util.Arrays;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code03_CherryBlossomViewing  
  * @description: 观赏樱花  
  * // 给定一个背包的容量t，一共有n种货物，并且给定每种货物的信息  
  * // 花费(cost)、价值(val)、数量(cnt)  
  * // 如果cnt == 0，代表这种货物可以无限选择  
  * // 如果cnt > 0，那么cnt代表这种货物的数量  
  * // 挑选货物的总容量在不超过t的情况下，返回能得到的最大价值  
  * // 背包容量不超过1000，每一种货物的花费都>0  
  * // 测试链接 : https://www.luogu.com.cn/problem/P1833  
  * @author: zs宝  
  * @create: 2025-09-09 20:55  
  * @Version 1.0  
  **/public class Code03_CherryBlossomViewing {  
     public static int MAXT = 1001;  
     public static int MAXN = 100001;  
     public static int[] val = new int[MAXN];  
     public static int[] costs = new int[MAXN];  
   
     public static int[] dp = new int[MAXN];  
   
     public static int hour1, minute1, hour2, minute2;  
     public static int time, n,m;  
   
     public static void main(String[] args) throws IOException {  
         BufferedReader buffer = new BufferedReader(new InputStreamReader(System.in));  
         StreamTokenizer in = new StreamTokenizer(buffer);  
         in.parseNumbers();  
         PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));  
         while (in.nextToken() != StreamTokenizer.TT_EOF) {  
             hour1 = (int) in.nval;  
             //跳过冒号  
             in.nextToken();  
             in.nextToken();  
             minute1=(int)in.nval;  
             in.nextToken();  
             hour2 = (int) in.nval;  
             //跳过冒号  
             in.nextToken();  
             in.nextToken();  
             minute2=(int)in.nval;  
   
             in.nextToken();  
             n=(int)in.nval;  
   
             if(minute2<minute1){  
                 hour2=hour2-1;  
                 minute2=minute2+60;  
             }  
             time=(hour2-hour1)*60+(minute2-minute1);  
             m=0;  
             for(int i=1,value,cost,cnt;i<=n;i++){  
                 in.nextToken();  
                 cost=(int)in.nval;  
                 in.nextToken();  
                 value=(int)in.nval;  
                 in.nextToken();  
                 cnt=(int)in.nval;  
                 if(cnt==0){  
                     cnt=MAXT;  
                 }  
   
                 for(int k=1;k<=cnt;k<<=1){  
                     val[++m]=value*k;  
                     costs[m]=cost*k;  
                     cnt-=k;  
                 }  
                 if(cnt>0){  
                     val[++m]=value*cnt;  
                     costs[m]=cost*cnt;  
                 }  
   
             }  
             out.println(compute());  
         }  
         out.flush();  
         out.close();  
         buffer.close();  
     }  
   
     public static int compute(){  
         Arrays.fill(dp,0,time+1,0);  
         for(int i=1;i<=m;i++){  
             for(int j=time;j>=costs[i];j--){  
                 dp[j]=Math.max(dp[j],dp[j-costs[i]]+val[i]);  
             }  
         }  
         return dp[time];  
     }  
 }

4、宝物筛选 -多重背包单调队列优化

题目描述一共有n种货物, 背包容量为t 每种货物的价值 (v[i])、重量 (w[i])、数量 (c[i]) 都给出请返回选择货物不超过背包容量的情况下，能得到的最大的价值

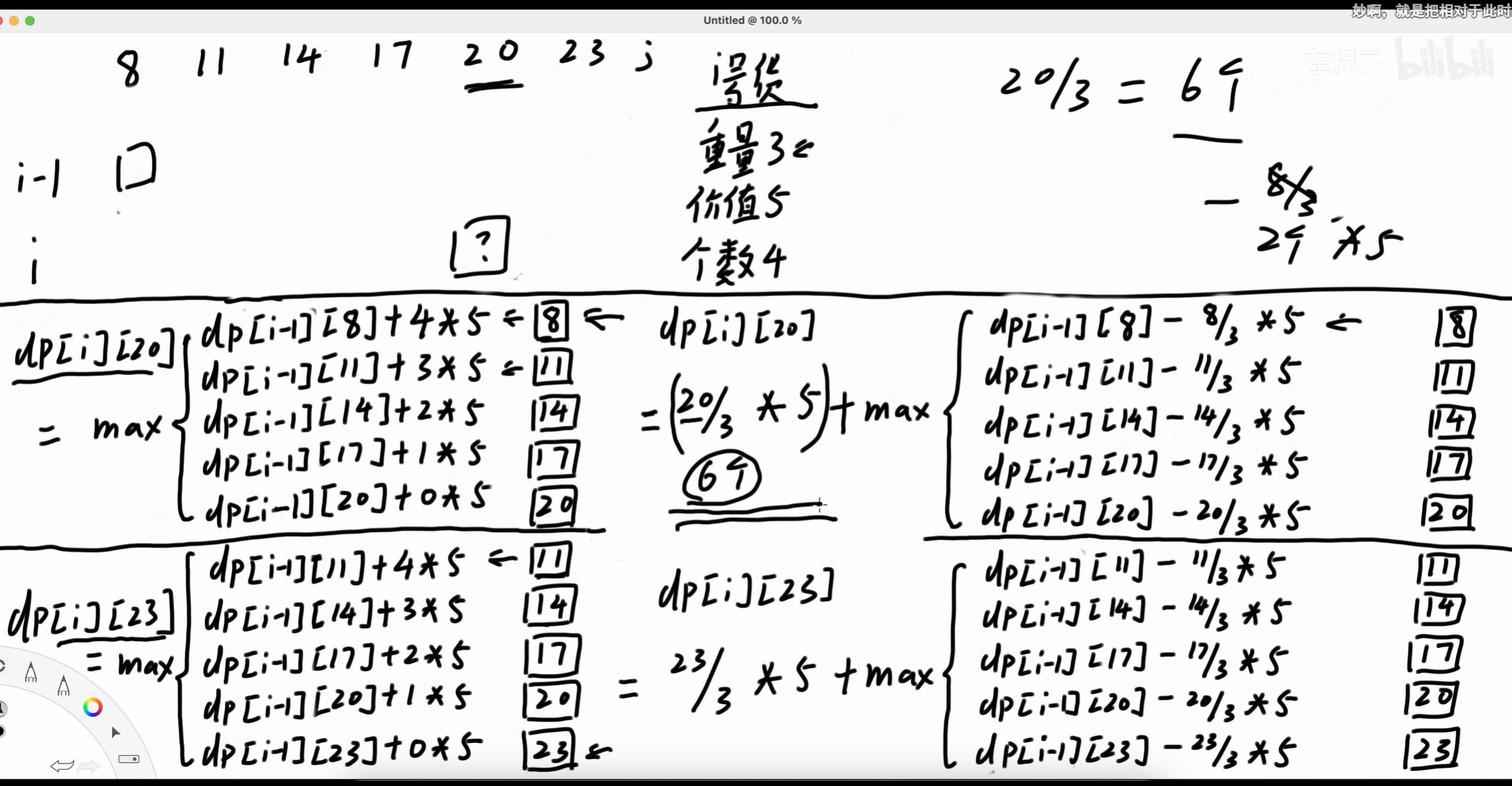
解题思路：

我们知道在多重背包的基础解法1、[宝物筛选](https://www.luogu.com.cn/problem/P1776) -多重背包不进行枚举优化上，我们是让 dp[i][j] 取的不要第i个商品，要1个i商品，要2个i商品... 要cnts[i]个i商品所能得到价值的的最大值，如上图左侧部分。
基础解法应对大多数甚至全部题目超时，也就是这不断的枚举过程找最大值而超时（枚举过程形成了第三个for循环）
而优化的点也就在如何简化这个枚举过程，如2、[宝物筛选](https://www.luogu.com.cn/problem/P1776) -二进制分组转化优化 (模版)、的利用二进制分组将多重背包转为01背包，但是这种方式看似没有了这个第三层的for枚举过程，但是却还是对第一层的物品数量进行了增加，只是将原本第三层的for枚举转移到了第一层的for枚举中，只不过其中枚举数量由原本的cnts[i]变为了log(cnts[i])。
有没有一种办法能够让我们每到达一个背包容量位置，就可以快速取出其中关于物品数量枚举的最大值呢? 并且还能随着背包容量位置的变化动态调整最大值位置（因为物品数量有限，背包容量位置不同，其j-weight[i] * cnts[i]位置也不同）？这就是需要空间换时间，而既能方便进出，还能快速取出范围内的最大值，这刚好可以利用单调队列来完成。
仔细观察上面图片，当当前背包容量j=20时，由于物品本身的代价，所以 dp[i][20] 只与20-K* weight[i]的背包容量有关，即不要第i件商品的背包容量20（dp[i-1][20]）, 要1件i物品的17(dp[i-1][17]), 14,11,8。我们发现这些数字的差值都为i物品的代价，因此这些数值求余第i件物品余数相同。这就是单调队列优化的前提，同余分组
但是我们仔细观察左边的式子，里面的关于要了多少个i物品要加多少i物品的价值（这个东西需要动态的求），这其中很多变量会随着背包容量位置发生变化，我们不希望这样，于是将左半边的式子转化为右半边的式子，左右的式子等价
单调队列会维持一个物品数量+1的窗口（要第i个物品，不要第i个物品），最左边为代价最大的时候，这个时候就和以往的单调队列没有区别，注意维持边界是否合理

代码如下

 package main.java.class075;  
   
 import java.io.*;  
 import java.util.Arrays;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code04_BoundedKnapsackWithMonotonicQueue  
  * @description: 多重背包单调队列优化  
  * // 宝物筛选  
  * // 一共有n种货物, 背包容量为t  
  * // 每种货物的价值(v[i])、重量(w[i])、数量(c[i])都给出  
  * // 请返回选择货物不超过背包容量的情况下，能得到的最大的价值  
  * // 测试链接 : https://www.luogu.com.cn/problem/P1776  
  * @author: zs宝  
  * @create: 2025-09-10 10:18  
  * @Version 1.0  
  **/public class Code04_BoundedKnapsackWithMonotonicQueue {  
     public static int MAXW=40001;  
     public static int MAXN=101;  
     public static int n,w;  
     public static int[] val=new int[MAXN];  
     public static int[] weight=new int[MAXN];  
     public static int[] cnts=new int[MAXN];  
     public static int[]dp=new int[MAXW];  
   
     public static int[]queue=new int[MAXW];  
     public static int l,r;  
   
   
     public static void main(String[] args) throws IOException {  
         BufferedReader buffer=new BufferedReader(new InputStreamReader(System.in));  
         StreamTokenizer in=new StreamTokenizer(buffer);  
         PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));  
         while (in.nextToken()!=StreamTokenizer.TT_EOF){  
             n=(int)in.nval;  
             in.nextToken();  
             w=(int)in.nval;  
             for(int i=1;i<=n;i++){  
                 in.nextToken();  
                 val[i]=(int)in.nval;  
                 in.nextToken();  
                 weight[i]=(int)in.nval;  
                 in.nextToken();  
                 cnts[i]=(int)in.nval;  
             }  
             out.println(compute1());  
         }  
         out.flush();  
         out.close();  
         buffer.close();  
     }  
   
   
     // 严格位置依赖的动态规划 + 单调队列优化枚举  
     public static int compute1(){  
         int[][]dp=new int[n+1][w+1];  
         for(int i=1;i<=n;i++){  
             //同余分组，背包容量/物品代价余数相同的为一组  
             for(int mod=0;mod<=Math.min(w,weight[i]-1);mod++){  
                 l=r=0;  
                 for(int j=mod;j<=w;j+=weight[i]){  
                     while(l<r && value1(dp,i,queue[r-1])<=value1(dp,i,j)){  
                         r--;  
                     }  
                     queue[r++]=j;  
                     if(queue[l]==j-weight[i]*(cnts[i]+1)){  
                         l++;  
                     }  
                     dp[i][j]=j/weight[i]*val[i]+value1(dp,i,queue[l]);  
                 }  
             }  
         }  
         return dp[n][w];  
     }  
   
     public  static int value1(int[][]dp,int i,int j){  
         return dp[i-1][j]-(j/weight[i])*val[i];  
     }  
   
     // 严格位置依赖的动态规划 + 单调队列优化枚举+空间压缩  
     public static int compute2(){  
         Arrays.fill(dp,0,w+1,0);  
         for(int i=1;i<=n;i++){  
             //同余分组，背包容量/物品代价余数相同的为一组  
             for(int mod=0;mod<=Math.min(w,weight[i]-1);mod++){  
                 l=r=0;  
                 //先让最初的分组指标进来  
                 for(int j=w-mod,cnt=1;j>=0 && cnt<=cnts[i];cnt++,j-=weight[i]){  
                     while(l<r && value2(i,queue[r-1])<+value2(i,j)){  
                         r--;  
                     }  
                     queue[r++]=j;  
                 }  
                 //开始dp  
                 for(int j=w-mod,enter=j-weight[i]*cnts[i];j>=0;j-=weight[i],enter-=weight[i]){  
                     //窗口进入enter指标位置，现在对于j位置的多重背包比较的序列已经全部到其  
                     if(enter>=0){  
                         while (l<r && value2(i,queue[r-1])<=value2(i,enter)){  
                             r--;  
                         }  
                         queue[r++]=enter;  
                     }  
   
                     dp[j]=j/weight[i]*val[i]+value2(i,queue[l]);  
                     //求下一轮的j时，最左位置值不能是当前j  
                     if(queue[l]==j){  
                         l++;  
                     }  
                 }  
             }  
         }  
         return dp[w];  
     }  
   
     public static int value2(int i,int j){  
         return dp[j]-(j/weight[i])*val[i];  
     }  
 }

5、能成功找零的钱数种类

题目描述：每一种货币都给定面值val[i]，和拥有的数量cnt[i] 想知道目前拥有的货币，在钱数为1、2、3…m时能找零成功的钱数有多少也就是说当钱数的范围是1~m 返回这个范围上有多少可以找零成功的钱数比如只有3元的货币，数量是5张 m = 10 那么在1~10范围上，只有钱数是3、6、9时，可以成功找零所以返回3表示有3种钱数可以找零成功

解题思路：

根据物品数量的题意转换为不同的背包问题

代码如下

 package main.java.class075;  
   
 import java.io.*;  
 import java.util.Arrays;  
   
 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code05_MixedKnapsack  
  * @description: 混合背包 + 多重背包普通窗口优化  
  * // 能成功找零的钱数种类  
  * // 每一种货币都给定面值val[i]，和拥有的数量cnt[i]  
  * // 想知道目前拥有的货币，在钱数为1、2、3...m时  
  * // 能找零成功的钱数有多少  
  * // 也就是说当钱数的范围是1~m  
  * // 返回这个范围上有多少可以找零成功的钱数  
  * // 比如只有3元的货币，数量是5张  
  * // m = 10  
  * // 那么在1~10范围上，只有钱数是3、6、9时，可以成功找零  
  * // 所以返回3表示有3种钱数可以找零成功  
  * // 测试链接 : http://poj.org/problem?id=1742  
  * @author: zs宝  
  * @create: 2025-09-10 20:27  
  * @Version 1.0  
  **/public class Code05_MixedKnapsack {  
     public static int MAXN = 101;  
   
     public static int MAXM = 100001;  
   
     public static int[] val = new int[MAXN];  
   
     public static int[] cnt = new int[MAXN];  
   
     public static boolean[] dp = new boolean[MAXM];  
   
     public static int n, m;  
   
     public static void main(String[] args) throws IOException {  
         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));  
         StreamTokenizer in = new StreamTokenizer(br);  
         PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));  
         while (in.nextToken() != StreamTokenizer.TT_EOF) {  
             n = (int) in.nval;  
             in.nextToken();  
             m = (int) in.nval;  
             if (n != 0 || m != 0) {  
                 for (int i = 1; i <= n; i++) {  
                     in.nextToken();  
                     val[i] = (int) in.nval;  
                 }  
                 for (int i = 1; i <= n; i++) {  
                     in.nextToken();  
                     cnt[i] = (int) in.nval;  
                 }  
                 out.println(compute());  
             }  
         }  
         out.flush();  
         out.close();  
         br.close();  
     }  
   
     public static int compute(){  
         Arrays.fill(dp,1,m+1,false);  
         dp[0]=true;  
         for(int i=1;i<=n;i++){  
             //01背包  
             if(cnt[i]==1){  
                 for(int j=m;j>=0;j--){  
                     if(dp[j-val[i]]){  
                         dp[j]=true;  
                     }  
                 }  
             }else if(val[i] *cnt[i]>m){  
                 //完全背包  
                 for(int j=val[i];j<=m;j++){  
                     if(dp[j-val[i]]){  
                         dp[j]=true;  
                     }  
                 }  
             } else {  
                 //多重背包  
                 for(int mod=0;mod<val[i];mod++){  
                     int trueCnt=0;  
                     for(int j=m-mod,size=0;j>=0 && size<=cnt[i];j-=val[i],size++){  
                         trueCnt+=dp[j]?1:0;  
                     }  
                     for(int j=m-mod,l=j-val[i]*(cnt[i]+1);j>=1;j-=val[i],l-=val[i]){  
                         if(dp[j]){  
                             trueCnt--;  
                         }else {  
                             if(trueCnt!=0){  
                                 dp[j]=true;  
                             }  
                         }  
                         if(l>=0){  
                             trueCnt+=dp[l]?1:0;  
                         }  
                     }  
                 }  
             }  
         }  
         int ans=0;  
         for(int i=1;i<=m;i++){  
             if(dp[i]){  
                 ans+=1;  
             }  
         }  
         return ans;  
     }  
 }

参考资料

左程云-算法通关系列-075

如果觉得文章对你有用，请随意赞赏

算法动态规划

动态规划10：背包dp-多重背包、混合背包

https://zshunbao.top/archives/dong-tai-gui-hua-10-bei-bao-dp-duo-chong-bei-bao-hun-he-bei-bao

作者

zs宝

发布于

2025-09-10

更新于

2025-09-10

许可协议

CC BY 4.0