关键思想

宽度优先遍历基本内容

Bfs 的特点是逐层扩散，从源头点到目标点扩散了几层，最短路就是多少

Bfs 可以使用的特征是任意两个节点之间的相互距离相同（无向图）

Bfs 开始时，可以是单个源头、也可以是多个源头

Bfs 频繁使用队列，形式可以是单点弹出或者整层弹出

Bfs 进行时，进入队列的节点需要标记状态，防止同一个节点重复进出队列

Bfs 进行时，可能会包含剪枝策略的设计

Bfs 是一个理解难度很低的算法，难点在于节点如何找到路、路的展开和剪枝设计

01 bfs

01bfs，适用于图中所有边的权重只有0和1两种值，求源点到目标点的最短距离 时间复杂度为 O(节点数量+边的数量)，为什么不能用传统bfs？ 流程如下：

1、distance[i]表示从源点到i点的最短距离，初始时所有点的distance设置为无穷大

2、源点进入双端队列，distance[源点]=0

3、双端队列 头部弹出 x，

  • A，如果x是目标点，返回distance[x]表示源点到目标点的最短距离

  • B，考察从x出发的每一条边，假设某边去y点，边权为w

    • 1）如果 distance[y] > distance[x] + w，处理该边；否则忽略该边

    • 2）处理时，更新distance[y] = distance[x] + w 如果w0，y从头部进入双端队列；如果w1，y从尾部进入双端队列

    • 3）考察完x出发的所有边之后，重复步骤3

4，双端队列为空停止

模版代码

普通 bfs

 class Solution {  
     public static int MAXM=101;  
     public static int MAXN=101;  
     public static int[][]queue=new int[MAXM*MAXN][2];  
     public static boolean[][]visit=new boolean[MAXN][MAXM];  
     public static int l,r;  
     // (x,y)  i来到0位置 : x + move[i], y + move[i+1] -> x - 1, y    // (x,y)  i来到1位置 : x + move[i], y + move[i+1] -> x, y + 1    // (x,y)  i来到2位置 : x + move[i], y + move[i+1] -> x + 1, y    // (x,y)  i来到3位置 : x + move[i], y + move[i+1] -> x, y - 1    public static int[]move=new int[]{-1,0,1,0,-1};  
   
     public int maxDistance(int[][] grid) {  
         int n=grid.length;  
         int m=grid[0].length;  
         l=0;  
         r=0;  
         int seas=0;  
         //初始化，寻找所有的陆地并标识，同时标识所有的海洋  
         for(int i=0;i<n;i++){  
             for(int j=0;j<m;j++){  
                 if(grid[i][j]==1){  
                     //标识并收集  
                     visit[i][j]=true;  
                     queue[r][0]=i;  
                     queue[r++][1]=j;  
                 }else{  
                     visit[i][j]=false;  
                     seas++;  
                 }  
             }  
         }  
         //如果全是陆地或者海洋，直接按照题意返回-1  
         if(seas==0 || seas==n*m){  
             return -1;  
         }  
         //接下来开始bfs  
         int level=0;  
         int size=0;  
         while(l<r){  
             level++;  
             size=r-l;  
             for(int i=0,x,y,nx,ny;i<size;i++){  
                 x=queue[l][0];  
                 y=queue[l++][1];  
                 //找到每块陆地旁边的海洋  
                 for(int j=0;j<4;j++){  
                     //上下左右分别遍历  
                     nx=x+move[j];  
                     ny=y+move[j+1];  
                     if(nx>=0 && nx<n && ny>=0 && ny<m && !visit[nx][ny]){  
                         visit[nx][ny]=true;  
                         queue[r][0]=nx;  
                         queue[r++][1]=ny;  
                     }  
                 }  
             }  
         }  
         return level-1;  
     }  
 }

01 bfs

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code03_MinimumObstacleRemovalToReachCorner  
  * @description:到达角落需要移除障碍物的最小数目  
  *  给你一个下标从 0 开始的二维整数数组 grid ，数组大小为 m x n  
  *  每个单元格都是两个值之一：  
  *  0 表示一个 空 单元格，  
  *  1 表示一个可以移除的 障碍物  
  *  你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。  
  *  现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1)  
  *  返回需要移除的障碍物的最小数目  
  *  测试链接 : https://leetcode.cn/problems/minimum-obstacle-removal-to-reach-corner/  
  * @author: zs宝  
  * @create: 2025-07-17 09:34  
  * @Version 1.0  
  **/  
 package main.java.class062;  
   
 import java.util.ArrayDeque;  
   
 public class Code03_MinimumObstacleRemovalToReachCorner {  
     class Solution {  
         public int minimumObstacles(int[][] grid) {  
             //四个方向前后左右的移动数组  
             int[] move ={ -1, 0, 1, 0, -1 };  
             int m = grid.length;  
             int n = grid[0].length;  
             //出发点到每个点的距离数组  
             int[][] distance = new int[m][n];  
             for (int i = 0; i < m; i++) {  
                 for (int j = 0; j < n; j++) {  
                     distance[i][j] = Integer.MAX_VALUE;  
                 }  
             }  
             //创建一个队列，这个队列中存放层次遍历的点  
             ArrayDeque<int[]> queue = new ArrayDeque<>();  
             //初始时存放出发点  
             queue.addFirst(new int[] { 0, 0 });  
             distance[0][0] = 0;  
             //接下来就是01bfs的重点  
             /**  
              1，distance[i]表示从源点到i点的最短距离，初始时所有点的distance设置为无穷大  
              2，源点进入双端队列，distance[源点]=0  
              3，双端队列 头部弹出 x，  
              A，如果x是目标点，返回distance[x]表示源点到目标点的最短距离  
              B，考察从x出发的每一条边，假设某边去y点，边权为w  
              1）如果 distance[y] > distance[x] + w，处理该边；否则忽略该边  
              2）处理时，更新distance[y] = distance[x] + w  
              如果w==0，y从头部进入双端队列；如果w==1，y从尾部进入双端队列  
              3）考察完x出发的所有边之后，重复步骤3  
              4，双端队列为空停止  
              */  
             while (!queue.isEmpty()) {  
                 //头部弹出  
                 int[] record = queue.pollFirst();  
                 int x = record[0];  
                 int y = record[1];  
                 //A，如果x是目标点，返回distance[x]表示源点到目标点的最短距离  
                 if (x == m - 1 && y == n - 1) {  
                     return distance[x][y];  
                 }  
                 /**  
                  B，考察从x出发的每一条边，假设某边去y点，边权为w  
                  1）如果 distance[y] > distance[x] + w，处理该边；否则忽略该边  
                  2）处理时，更新distance[y] = distance[x] + w  
                  如果w==0，y从头部进入双端队列；如果w==1，y从尾部进入双端队列  
                  3）考察完x出发的所有边之后，重复步骤3  
                  */                for (int i = 0; i < 4; i++) {  
                     int nx = x + move[i];  
                     int ny = y + move[i + 1];  
                     if (nx >= 0 && nx < m && ny >= 0 && ny < n && distance[nx][ny] > distance[x][y] + grid[nx][ny]) {  
                         distance[nx][ny] = distance[x][y] + grid[nx][ny];  
                         if (grid[nx][ny] == 0) {  
                             queue.addFirst(new int[] { nx, ny });  
                         } else {  
                             queue.addLast(new int[] { nx, ny });  
                         }  
                     }  
                 }  
             }  
             return -1;  
         }  
     }  
 }

例题

1、地图分析

题目描述： 你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

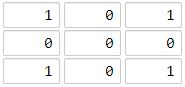
输入：grid = [[1,0,1],[0,0,0],[1,0,1]] 输出：2 解释： 海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

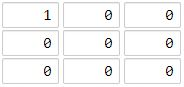
输入：grid = [[1,0,0],[0,0,0],[0,0,0]] 输出：4 解释： 海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

提示：

  • n == grid.length

  • n == grid[i].length

  • 1 <= n <= 100

  • grid[i][j] 不是 0 就是 1

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 1162 + 地图分析

🧠 题目关键词（原文关键词）

海洋、陆地、最远距离、曼哈顿距离

🧩 抽象问题类型（题目本质）

多源 BFS（从所有陆地出发传播，寻找最远海洋点）

🔍 数据规模 / 限制

1 ≤ n ≤ 100，gridi ∈ {0, 1}

🧭 我的初步思路

枚举每个海洋格子，暴力搜索到所有陆地求最小值，再取最大（TLE）

✅ 正确解法类型

多源 BFS（将所有陆地作为起点，一层层扩展

❗ 没想到的原因

没意识到可以从所有陆地 同时开始 反向传播距离，而不是每个海洋单独搜索

📦 归入的题型分类

网格 BFS 类、最短距离传播类、图论（无权图）类

🧠 触发词（以后遇到就联想）

“离最近的某种点最远 + 距离 + 多起点” → 多源 BFS

🧪 解法一句话总结

将所有陆地加入队列，从陆地出发做多源 BFS 扩展到海洋，最后一层就是最大距离

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code01_AsFarFromLandAsPossible  
  * @description: 地图分析  
  * // 你现在手里有一份大小为 n x n 的 网格 grid  
  * // 上面的每个 单元格 都用 0 和 1 标记好了其中 0 代表海洋，1 代表陆地。  
  * // 请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的  
  * // 并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。  
  * // 我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：  
  * // (x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。  
  * // 测试链接 : https://leetcode.cn/problems/as-far-from-land-as-possible/  
  * @author: zs宝  
  * @create: 2025-07-14 11:23  
  * @Version 1.0  
  **/  
 package main.java.class062;  
   
 public class Code01_AsFarFromLandAsPossible {  
     class Solution {  
         public static int MAXM=101;  
         public static int MAXN=101;  
         public static int[][]queue=new int[MAXM*MAXN][2];  
         public static boolean[][]visit=new boolean[MAXN][MAXM];  
         public static int l,r;  
         // (x,y)  i来到0位置 : x + move[i], y + move[i+1] -> x - 1, y        // (x,y)  i来到1位置 : x + move[i], y + move[i+1] -> x, y + 1        // (x,y)  i来到2位置 : x + move[i], y + move[i+1] -> x + 1, y        // (x,y)  i来到3位置 : x + move[i], y + move[i+1] -> x, y - 1        public static int[]move=new int[]{-1,0,1,0,-1};  
   
         public int maxDistance(int[][] grid) {  
             int n=grid.length;  
             int m=grid[0].length;  
             l=0;  
             r=0;  
             int seas=0;  
             //初始化，寻找所有的陆地并标识，同时标识所有的海洋  
             for(int i=0;i<n;i++){  
                 for(int j=0;j<m;j++){  
                     if(grid[i][j]==1){  
                         //标识并收集  
                         visit[i][j]=true;  
                         queue[r][0]=i;  
                         queue[r++][1]=j;  
                     }else{  
                         visit[i][j]=false;  
                         seas++;  
                     }  
                 }  
             }  
             //如果全是陆地或者海洋，直接按照题意返回-1  
             if(seas==0 || seas==n*m){  
                 return -1;  
             }  
             //接下来开始bfs  
             int level=0;  
             int size=0;  
             while(l<r){  
                 level++;  
                 size=r-l;  
                 for(int i=0,x,y,nx,ny;i<size;i++){  
                     x=queue[l][0];  
                     y=queue[l++][1];  
                     //找到每块陆地旁边的海洋  
                     for(int j=0;j<4;j++){  
                         //上下左右分别遍历  
                         nx=x+move[j];  
                         ny=y+move[j+1];  
                         if(nx>=0 && nx<n && ny>=0 && ny<m && !visit[nx][ny]){  
                             visit[nx][ny]=true;  
                             queue[r][0]=nx;  
                             queue[r++][1]=ny;  
                         }  
                     }  
                 }  
             }  
             return level-1;  
         }  
     }  
 }

2、贴纸拼词

题目描述： 我们有 n 种不同的贴纸。每个贴纸上都有一个小写的英文单词。

您想要拼写出给定的字符串 target ，方法是从收集的贴纸中切割单个字母并重新排列它们。如果你愿意，你可以多次使用每个贴纸，每个贴纸的数量是无限的。

返回你需要拼出 target 的最小贴纸数量。如果任务不可能，则返回 -1 。

注意：在所有的测试用例中，所有的单词都是从 1000 个最常见的美国英语单词中随机选择的，并且 target 被选择为两个随机单词的连接。

示例 1：

输入： stickers = ["with","example","science"], target = "thehat" 输出：3 解释： 我们可以使用 2 个 "with" 贴纸，和 1 个 "example" 贴纸。 把贴纸上的字母剪下来并重新排列后，就可以形成目标 “thehat“ 了。 此外，这是形成目标字符串所需的最小贴纸数量。

示例 2:

输入：stickers = ["notice","possible"], target = "basicbasic" 输出：-1 解释：我们不能通过剪切给定贴纸的字母来形成目标“basicbasic”。

提示:

  • n == stickers.length

  • 1 <= n <= 50

  • 1 <= stickers[i].length <= 10

  • 1 <= target.length <= 15

  • stickers[i] 和 target 由小写英文单词组成

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 691 + 贴纸拼词

🧠 题目关键词（原文关键词）

贴纸、拼单词、剪字母、无限使用、最小贴纸数、不能拼出返回 -1

🧩 抽象问题类型（题目本质）

Bfs+剪枝

🔍 数据规模 / 限制

N ≤ 50，target. Length ≤ 15，每个 sticker. Length ≤ 10，NP 难问题

🧭 我的初步思路

无想法

✅ 正确解法类型

Bfs+剪枝

❗ 没想到的原因

分析不出来

📦 归入的题型分类

Bfs

🧠 触发词（以后遇到就联想）

🧪 解法一句话总结

将贴纸和 target 中的字符按照字符顺序排序，而后利用 bfs 不断减少 target 中的字符，直到为空

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code02_StickersToSpellWord  
  * @description: 贴纸拼词  
  * // 我们有 n 种不同的贴纸。每个贴纸上都有一个小写的英文单词。  
  * // 您想要拼写出给定的字符串 target ，方法是从收集的贴纸中切割单个字母并重新排列它们  
  * // 如果你愿意，你可以多次使用每个贴纸，每个贴纸的数量是无限的。  
  * // 返回你需要拼出 target 的最小贴纸数量。如果任务不可能，则返回 -1  
  * // 注意：在所有的测试用例中，所有的单词都是从 1000 个最常见的美国英语单词中随机选择的  
  * // 并且 target 被选择为两个随机单词的连接。  
  * // 测试链接 : https://leetcode.cn/problems/stickers-to-spell-word/  
  * @author: zs宝  
  * @create: 2025-07-16 17:26  
  * @Version 1.0  
  **/  
 package main.java.class062;  
   
 import java.util.ArrayList;  
 import java.util.Arrays;  
 import java.util.HashSet;  
   
 public class Code02_StickersToSpellWord {  
     class Solution {  
         public static int MAXN = 401;  
         public static String[] queue = new String[MAXN];  
         public static int l, r;  
         //用来判断某个贴纸是否使用过  
         public static HashSet<String> visits = new HashSet<>();  
         //只有小写字母，创建一个图，其中存储包含改小写字母的所有贴纸  
         public static ArrayList<ArrayList<String>> graph = new ArrayList<>();  
         // 下标0 -> a  
         // 下标1 -> b  
         // 下标2 -> c  
         // ...        // 下标25 -> z  
         static {  
             for (int i = 0; i < 26; i++) {  
                 graph.add(new ArrayList<>());  
             }  
         }  
   
         public int minStickers(String[] stickers, String target) {  
             //初始化，图和判断贴纸是否使用的都清空  
             for (int i = 0; i < 26; i++) {  
                 graph.get(i).clear();  
             }  
             visits.clear();  
             //将所有贴纸放进对应的图中  
             for (String str : stickers) {  
                 //先将贴纸的所有字符排序  
                 str = sort(str);  
                 for (int i = 0; i < str.length(); i++) {  
                     //将包含某个字母的贴纸加入对应的图中，但是当多个相同字符相邻时如aaa,贴纸不可以重复添加多次  
                     if (i == 0 || str.charAt(i) != str.charAt(i - 1)) {  
                         graph.get(str.charAt(i) - 'a').add(str);  
                     }  
                 }  
             }  
             target = sort(target);  
             visits.add(target);  
             //接下来开始bfs的过程  
             l = 0;  
             r = 0;  
             int level = 1;  
             queue[r++] = target;  
             while (l < r) {  
                 int size = r - l;  
                 for (int i = 0; i < size; i++) {  
                     String cur = queue[l++];  
                     //这里有一点剪枝的思想在其中，我们按照当前剩余字符cur的第一个字符来看graph中的字符，从而减少每一次的遍历贴纸数  
                     for (String str : graph.get(cur.charAt(0) - 'a')) {  
                         String next = next(cur, str);  
                         if (next.equals("")) {  
                             return level;  
                         } else if (!visits.contains(next)) {  
                             visits.add(next);  
                             queue[r++] = next;  
                         }  
                     }  
                 }  
                 level++;  
             }  
             //bfs完后还没有返回，则说明先有贴纸不足以拼出target  
             return -1;  
         }  
   
         public static String sort(String s) {  
             char[] str = s.toCharArray();  
             Arrays.sort(str);  
             return String.valueOf(str);  
         }  
   
         //当t中的字符减掉s中的共同字符，还剩下那些字符  
         public String next(String t, String s) {  
             StringBuilder builder = new StringBuilder();  
             for (int i = 0, j = 0; i < t.length();) {  
                 //如果s已经遍历玩，而t还没有，那就将t中剩余的字符全部加入builder中去  
                 if (j == s.length()) {  
                     builder.append(t.charAt(i++));  
                 } else {  
                     if (t.charAt(i) < s.charAt(j)) {  
                         builder.append(t.charAt(i));  
                         i++;  
                     } else if (t.charAt(i) > s.charAt(j)) {  
                         j++;  
                     } else {  
                         i++;  
                         j++;  
                     }  
                 }  
   
             }  
             return builder.toString();  
         }  
     }  
 }

3、到达角落需要移除障碍物的最小数目

题目描述： 给你一个下标从 0 开始的二维整数数组 grid ，数组大小为 m x n 。每个单元格都是两个值之一：

  • 0 表示一个 空 单元格，

  • 1 表示一个可以移除的 障碍物 。

你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。

现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ，返回需要移除的障碍物的 最小 数目。

示例 1：

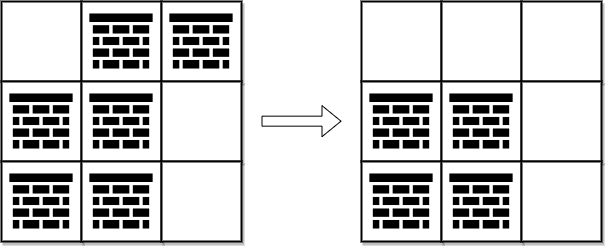
输入：grid = [[0,1,1],[1,1,0],[1,1,0]] 输出：2 解释：可以移除位于 (0, 1) 和 (0, 2) 的障碍物来创建从 (0, 0) 到 (2, 2) 的路径。 可以证明我们至少需要移除两个障碍物，所以返回 2 。 注意，可能存在其他方式来移除 2 个障碍物，创建出可行的路径。

示例 2：

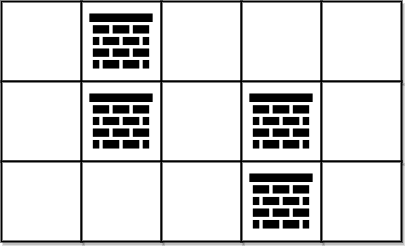
输入：grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]] 输出：0 解释：不移除任何障碍物就能从 (0, 0) 到 (2, 4) ，所以返回 0 。

提示：

  • m == grid.length

  • n == grid[i].length

  • 1 <= m, n <= 105

  • 2 <= m * n <= 105

  • grid[i][j] 为 0 或 1

  • grid[0][0] == grid[m - 1][n - 1] == 0

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 2290 + 到达角落需要移除障碍物的最小数目

🧠 题目关键词（原文关键词）

二维数组 grid 只有 1 和 0，上下左右移动，出发点到目标点需要要移除的障碍物的最小数目

🧩 抽象问题类型（题目本质）

权重为 0/1 的最短路径搜索（01 bfs）

🔍 数据规模 / 限制

M × n ≤ 10⁵，gridi ∈ {0, 1}，起点终点都为 0

🧭 我的初步思路

无想法

✅ 正确解法类型

01 bfs+双端队列

❗ 没想到的原因

没有把题目类型抽象成权重为 0/1 的最短路径搜索

📦 归入的题型分类

图论类、最短路径、权重图、0-1 BFS、Dijkstra 模板题

🧠 触发词（以后遇到就联想）

“网格 + 最小代价 + 权重为 0/1” → 想到 0-1 BFS

🧪 解法一句话总结

将 grid 视为 0-1 权图，用 deque 实现 0-1 BFS，每次优先走不需移除的路径

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code03_MinimumObstacleRemovalToReachCorner  
  * @description:到达角落需要移除障碍物的最小数目  
  *  给你一个下标从 0 开始的二维整数数组 grid ，数组大小为 m x n  
  *  每个单元格都是两个值之一：  
  *  0 表示一个 空 单元格，  
  *  1 表示一个可以移除的 障碍物  
  *  你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。  
  *  现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1)  
  *  返回需要移除的障碍物的最小数目  
  *  测试链接 : https://leetcode.cn/problems/minimum-obstacle-removal-to-reach-corner/  
  * @author: zs宝  
  * @create: 2025-07-17 09:34  
  * @Version 1.0  
  **/  
 package main.java.class062;  
   
 import java.util.ArrayDeque;  
   
 public class Code03_MinimumObstacleRemovalToReachCorner {  
     class Solution {  
         public int minimumObstacles(int[][] grid) {  
             //四个方向前后左右的移动数组  
             int[] move ={ -1, 0, 1, 0, -1 };  
             int m = grid.length;  
             int n = grid[0].length;  
             //出发点到每个点的距离数组  
             int[][] distance = new int[m][n];  
             for (int i = 0; i < m; i++) {  
                 for (int j = 0; j < n; j++) {  
                     distance[i][j] = Integer.MAX_VALUE;  
                 }  
             }  
             //创建一个队列，这个队列中存放层次遍历的点  
             ArrayDeque<int[]> queue = new ArrayDeque<>();  
             //初始时存放出发点  
             queue.addFirst(new int[] { 0, 0 });  
             distance[0][0] = 0;  
             //接下来就是01bfs的重点  
             /**  
              1，distance[i]表示从源点到i点的最短距离，初始时所有点的distance设置为无穷大  
              2，源点进入双端队列，distance[源点]=0  
              3，双端队列 头部弹出 x，  
              A，如果x是目标点，返回distance[x]表示源点到目标点的最短距离  
              B，考察从x出发的每一条边，假设某边去y点，边权为w  
              1）如果 distance[y] > distance[x] + w，处理该边；否则忽略该边  
              2）处理时，更新distance[y] = distance[x] + w  
              如果w==0，y从头部进入双端队列；如果w==1，y从尾部进入双端队列  
              3）考察完x出发的所有边之后，重复步骤3  
              4，双端队列为空停止  
              */  
             while (!queue.isEmpty()) {  
                 //头部弹出  
                 int[] record = queue.pollFirst();  
                 int x = record[0];  
                 int y = record[1];  
                 //A，如果x是目标点，返回distance[x]表示源点到目标点的最短距离  
                 if (x == m - 1 && y == n - 1) {  
                     return distance[x][y];  
                 }  
                 /**  
                  B，考察从x出发的每一条边，假设某边去y点，边权为w  
                  1）如果 distance[y] > distance[x] + w，处理该边；否则忽略该边  
                  2）处理时，更新distance[y] = distance[x] + w  
                  如果w==0，y从头部进入双端队列；如果w==1，y从尾部进入双端队列  
                  3）考察完x出发的所有边之后，重复步骤3  
                  */                for (int i = 0; i < 4; i++) {  
                     int nx = x + move[i];  
                     int ny = y + move[i + 1];  
                     if (nx >= 0 && nx < m && ny >= 0 && ny < n && distance[nx][ny] > distance[x][y] + grid[nx][ny]) {  
                         distance[nx][ny] = distance[x][y] + grid[nx][ny];  
                         if (grid[nx][ny] == 0) {  
                             queue.addFirst(new int[] { nx, ny });  
                         } else {  
                             queue.addLast(new int[] { nx, ny });  
                         }  
                     }  
                 }  
             }  
             return -1;  
         }  
     }  
 }

4、使网格图至少有一条有效路径的最小代价

题目描述： 给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字，对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况：

  • 1 ，下一步往右走，也就是你会从 grid[i][j] 走到 grid[i][j + 1]

  • 2 ，下一步往左走，也就是你会从 grid[i][j] 走到 grid[i][j - 1]

  • 3 ，下一步往下走，也就是你会从 grid[i][j] 走到 grid[i + 1][j]

  • 4 ，下一步往上走，也就是你会从 grid[i][j] 走到 grid[i - 1][j]

注意网格图中可能会有 无效数字 ，因为它们可能指向 grid 以外的区域。

一开始，你会从最左上角的格子 (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0) 出发，每一步都顺着数字对应方向走，最终在最右下角的格子 (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。

你可以花费 cost = 1 的代价修改一个格子中的数字，但每个格子中的数字 只能修改一次 。

请你返回让网格图至少有一条有效路径的最小代价。

示例 1：

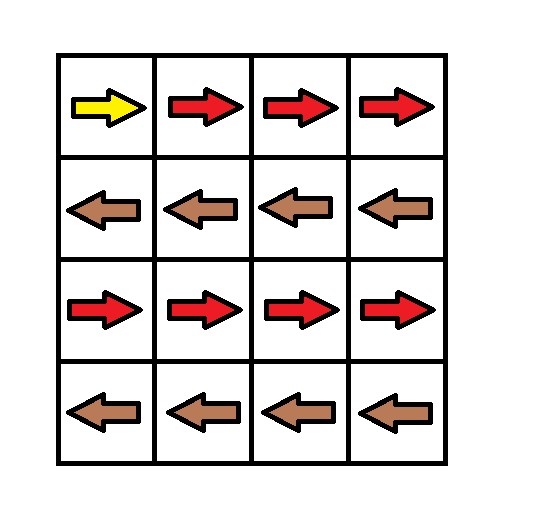
输入：grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]] 输出：3 解释：你将从点 (0, 0) 出发。 到达 (3, 3) 的路径为： (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) 花费代价 cost = 1 使方向向下 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) 花费代价 cost = 1 使方向向下 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) 花费代价 cost = 1 使方向向下 --> (3, 3) 总花费为 cost = 3.

示例 2：

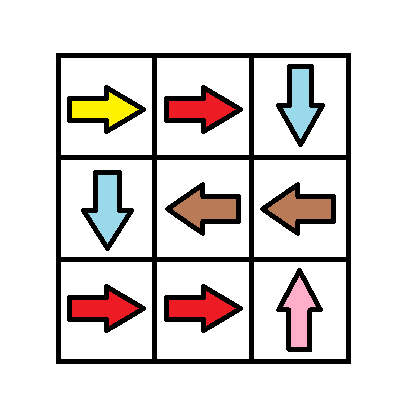
输入：grid = [[1,1,3],[3,2,2],[1,1,4]] 输出：0 解释：不修改任何数字你就可以从 (0, 0) 到达 (2, 2) 。

示例 3：

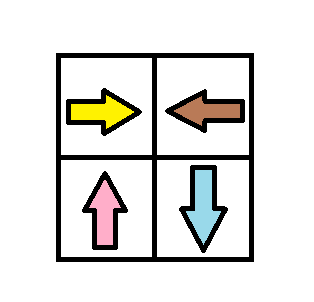
输入：grid = [[1,2],[4,3]] 输出：1

示例 4：

输入：grid = [[2,2,2],[2,2,2]] 输出：3

示例 5：

输入：grid = [[4]] 输出：0

提示：

  • m == grid.length

  • n == grid[i].length

  • 1 <= m, n <= 100

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 1368 + 使网格图至少有一条有效路径的最小代价

🧠 题目关键词（原文关键词）

网格图、方向修改、代价、路径、从左上到右下、最小修改次数

🧩 抽象问题类型（题目本质）

0-1 最短路径问题（每步代价为 0 或 1）→ 图上最短路径

🔍 数据规模 / 限制

1 ≤ m, n ≤ 100；gridi ∈ {1,2,3,4}（向右/左/下/上）

🧭 我的初步思路

无思路

✅ 正确解法类型

01 bfs

❗ 没想到的原因

没意识到图边权值只有 0/1，可以用 0-1 BFS 做到线性时间；没有从“修改”转化为“权值”建图思想

📦 归入的题型分类

01 bfs

🧠 触发词（以后遇到就联想）

“每次可以修改 / 改动的代价是 0 或 1” → 权值为 0/1 的图 → 0-1 BFS |

🧪 解法一句话总结

将每个格子看作图的点，合法方向是 0 代价，错误方向是 1 代价，使用 0-1 BFS 计算最短路径代价

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code04_MinimumCostToMakeAtLeastOneValidPath  
  * @description:使网格图至少有一条有效路径的最小代价  
  * // 给你一个 m * n 的网格图 grid 。 grid 中每个格子都有一个数字  
  * // 对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况：  
  * // 1 ，下一步往右走，也就是你会从 grid[i][j] 走到 grid[i][j + 1]  
  * // 2 ，下一步往左走，也就是你会从 grid[i][j] 走到 grid[i][j - 1]  
  * // 3 ，下一步往下走，也就是你会从 grid[i][j] 走到 grid[i + 1][j]  
  * // 4 ，下一步往上走，也就是你会从 grid[i][j] 走到 grid[i - 1][j]  
  * // 注意网格图中可能会有 无效数字 ，因为它们可能指向 grid 以外的区域  
  * // 一开始，你会从最左上角的格子 (0,0) 出发  
  * // 我们定义一条 有效路径 为从格子 (0,0) 出发，每一步都顺着数字对应方向走  
  * // 最终在最右下角的格子 (m - 1, n - 1) 结束的路径  
  * // 有效路径 不需要是最短路径  
  * // 你可以花费1的代价修改一个格子中的数字，但每个格子中的数字 只能修改一次  
  * // 请你返回让网格图至少有一条有效路径的最小代价  
  * // 测试链接 : https://leetcode.cn/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/  
  * @author: zs宝  
  * @create: 2025-07-18 11:00  
  * @Version 1.0  
  **/  
 package main.java.class062;  
   
 import java.util.ArrayDeque;  
   
 public class Code04_MinimumCostToMakeAtLeastOneValidPath {  
     class Solution {  
         public int minCost(int[][] grid) {  
             //表示索引1位置右走，2左，3下，4上  
             int[][]move={{},{0,1},{0,-1},{1,0},{-1,0}};  
             int m=grid.length;  
             int n=grid[0].length;  
             int[][]distace=new int[m][n];  
             for(int i=0;i<m;i++){  
                 for(int j=0;j<n;j++){  
                     distace[i][j]=Integer.MAX_VALUE;  
                 }  
             }  
             //构建双端队列  
             ArrayDeque<int[]> queue=new ArrayDeque<>();  
             queue.addFirst(new int[]{0,0});  
             distace[0][0]=0;  
             while(!queue.isEmpty()){  
                 int[]record=queue.pollFirst();  
                 int x=record[0];  
                 int y=record[1];  
                 if(x==m-1 && y==n-1){  
                     return distace[x][y];  
                 }  
                 for(int i=1;i<=4;i++){  
                     //注意这一步，这里就是本题对应的01dfs的题目分析转化为抽象模型的而关键  
                     //若当前方向与grid本来的方向同，那就是0，否则就为1  
                     int weight=grid[x][y]!=i?1:0;  
                     int nx=move[i][0]+x;  
                     int ny=move[i][1]+y;  
                     if(nx>=0 && nx<m && ny>=0 && ny<n && distace[nx][ny]>distace[x][y]+weight){  
                         distace[nx][ny]=distace[x][y]+weight;  
                         if(weight==0){  
                             queue.addFirst(new int[]{nx,ny});  
                         }else{  
                             queue.addLast(new int[]{nx,ny});  
                         }  
                     }  
                 }  
             }  
             return -1;  
         }  
     }  
 }

5、接雨水Ⅱ

题目描述： 给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1:

输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] 输出: 4 解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

示例 2:

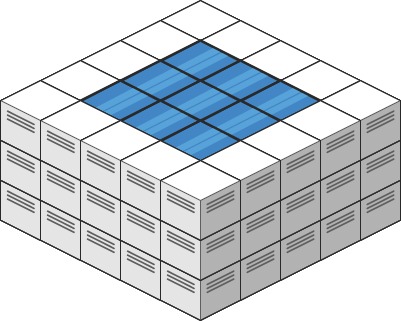
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]] 输出: 10

提示:

  • m == heightMap.length

  • n == heightMap[i].length

  • 1 <= m, n <= 200

  • 0 <= heightMap[i][j] <= 2 * 104

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 407 + 接雨水Ⅱ

🧠 题目关键词（原文关键词）

二维矩阵，图中形状最多能接多少体积的雨水

🧩 抽象问题类型（题目本质）

从边界向内扩展的“最小围栏”模型（最小堆模拟围栏高度 + BFS 扩展）

🔍 数据规模 / 限制

- m == heightMap.length - n == heightMap[i].length - 1 <= m, n <= 200 - 0 <= heightMap[i][j] <= 2 * 104

🧭 我的初步思路

从中间向外扩展，找到四周每个方向比其大的的最大值，在选择四个方向最大值中较小的那个，但是在向四周扩展的图中如果有比当前值小的那个，可以链接起来，链接起来若到边缘，则当前点无法接受雨水

✅ 正确解法类型

小根堆+bfs

❗ 没想到的原因

从内向外看当前点能否接雨水，接多少雨水，过程复杂且不好判定

📦 归入的题型分类

小根堆+bfs

🧠 触发词（以后遇到就联想）

二维高度图 + “围住蓄水” + 体积 → 从边界开始堆扩展，围栏模型 → 最小堆 + BFS

🧪 解法一句话总结

从矩阵最外层开始加入小根堆，从外向内扩展，每次弹出小根堆中的顶点进行 bfs 扩展，每次扩展的四个方向上的点，加入小根堆，但是加入小根堆时，其中的水线是要比较的，选择被扩展点的矩阵高度和扩展点的水线之间较大的那个

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code05_TrappingRainWaterII  
  * @description:二维接雨水  
  * // 给你一个 m * n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度  
  * // 请计算图中形状最多能接多少体积的雨水。  
  * // 测试链接 : https://leetcode.cn/problems/trapping-rain-water-ii/  
  * @author: zs宝  
  * @create: 2025-07-19 08:30  
  * @Version 1.0  
  **/  
 package main.java.class062;  
   
 import java.util.PriorityQueue;  
   
 public class Code05_TrappingRainWaterII {  
     class Solution {  
         public int trapRainWater(int[][] heightMap) {  
             int[]move={-1,0,1,0,-1};  
             int m=heightMap.length;  
             int n=heightMap[0].length;  
             //小根堆，0代表坐标x，1代表坐标y，2代表水线高度  
             PriorityQueue<int[]> heap=new PriorityQueue<>((a, b)->a[2]-b[2]);  
             boolean[][]visited=new boolean[m][n];  
             for(int i=0;i<m;i++){  
                 for(int j=0;j<n;j++){  
                     //如果是矩阵边缘，将其加入小顶堆，从外向里看，而不是从里向外看  
                     //最开始的想法就是从里向外看，很复杂，不好判断某个位置到底能不能接水，而反过来从边缘最小处向内看，就容易思考很多  
                     if(i==0 || i==m-1 || j==0 || j==n-1){  
                         visited[i][j]=true;  
                         heap.add(new int[]{i,j,heightMap[i][j]});  
                     }else{  
                         visited[i][j]=false;  
                     }  
                 }  
             }  
             int ans=0;  
             while(!heap.isEmpty()){  
                 int[]record=heap.poll();  
                 int x=record[0];  
                 int y=record[1];  
                 int w=record[2];  
                 ans+=w-heightMap[x][y];  
                 //开始bfs向四周扩散寻找  
                 for(int i=0;i<4;i++){  
                     int nx=x+move[i];  
                     int ny=y+move[i+1];  
                     if(nx>=0 && nx<m && ny>=0 && ny<n && !visited[nx][ny]){  
                         //将四周的点加入小根堆中  
                         //但是要注意其中小根堆里的水线需要当前位置的高度和引起这个点进堆的点的水线进行比较，选择大的那个  
                         heap.add(new int[]{nx,ny,Math.max(w,heightMap[nx][ny])});  
                         visited[nx][ny]=true;  
                     }  
                 }  
   
             }  
             return ans;  
         }  
     }  
 }

6、单词接龙Ⅱ

题目描述： 按字典 wordList 完成从单词 beginWord 到单词 endWord 转化，一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> ... -> sk 这样的单词序列，并满足：

  • 每对相邻的单词之间仅有单个字母不同。

  • 转换过程中的每个单词 si（1 <= i <= k）必须是字典 wordList 中的单词。注意，beginWord 不必是字典 wordList 中的单词。

  • sk == endWord

给你两个单词 beginWord 和 endWord ，以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, ..., sk] 的形式返回。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] 输出：[["hit","hot","dot","dog","cog"],["hit","hot","lot","log","cog"]] 解释：存在 2 种最短的转换序列： "hit" -> "hot" -> "dot" -> "dog" -> "cog" "hit" -> "hot" -> "lot" -> "log" -> "cog"

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"] 输出：[] 解释：endWord "cog" 不在字典 wordList 中，所以不存在符合要求的转换序列。

提示：

  • 1 <= beginWord.length <= 5

  • endWord.length == beginWord.length

  • 1 <= wordList.length <= 500

  • wordList[i].length == beginWord.length

  • beginWord、endWord 和 wordList[i] 由小写英文字母组成

  • beginWord != endWord

  • wordList 中的所有单词 互不相同

项目名称

内容填写（每道题一行填写）

📘 题目编号 / 标题

LeetCode 126 + 单词接龙Ⅱ

🧠 题目关键词（原文关键词）

按字典 wordList 完成从单词 beginWord 到单词 endWord 转化，相邻的单词之间仅有单个字母不同，找出并返回所有从 beginWord 到 endWord 的 最短转换序列

🧩 抽象问题类型（题目本质）

转换单词问题，求的所有最短路径

🔍 数据规模 / 限制

1 ≤ beginWord.length ≤ 5，1 ≤ wordList.length ≤ 500

🧭 我的初步思路

无思路

✅ 正确解法类型

Bfs+反向建图

❗ 没想到的原因

没 I 型那轨道 bfs 找到目标单词只要词典的单词只出现在某一层也只出现一次，即上层出现的单词下一层不能出现，那么找到的路径就是最短的

📦 归入的题型分类

图搜索类、BFS 类、回溯类、路径搜索类

🧠 触发词（以后遇到就联想）

从单词 A->B, 每次只能改变一个单词--->bfs+反向建图

🧪 解法一句话总结

Bfs 找到最短路径的过程中反向建图，利用反向图进行 dfs 搜集最短路径

 /**  
  * @program: ZuoChengxunAlgorithmClass  
  * @ClassName Code06_WordLadderII  
  * @description:单词接龙 II  
  * // 按字典 wordList 完成从单词 beginWord 到单词 endWord 转化  
  * // 一个表示此过程的 转换序列 是形式上像  
  * // beginWord -> s1 -> s2 -> ... -> sk 这样的单词序列，并满足：  
  * // 每对相邻的单词之间仅有单个字母不同  
  * // 转换过程中的每个单词 si（1 <= i <= k）必须是字典 wordList 中的单词  
  * // 注意，beginWord 不必是字典 wordList 中的单词  
  * // sk == endWord  
  * // 给你两个单词 beginWord 和 endWord ，以及一个字典 wordList  
  * // 请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列  
  * // 如果不存在这样的转换序列，返回一个空列表  
  * // 每个序列都应该以单词列表 [beginWord, s1, s2, ..., sk] 的形式返回  
  * // 测试链接 : https://leetcode.cn/problems/word-ladder-ii/  
  * @author: zs宝  
  * @create: 2025-07-19 10:24  
  * @Version 1.0  
  **/  
 package main.java.class062;  
   
 import java.util.*;  
   
 public class Code06_WordLadderII {  
     class Solution {  
         //记录给的所有字典里的单词，加速查找过程  
         public static HashSet<String> dic;  
         //当前层有哪些词典里的单词  
         public static HashSet<String> curLevel = new HashSet<>();  
         //下一层可以由当前层的单词改变一个字母，在词典中有哪些单词  
         public static HashSet<String> nextLevel = new HashSet<>();  
         //建图,反向图  
         public static HashMap<String, ArrayList<String>> graph = new HashMap<>();  
         //记录可以达成转换的一条路径  
         public static LinkedList<String> path = new LinkedList<>();  
         //记录最后的答案  
         public static List<List<String>> ans = new ArrayList<>();  
   
         public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {  
             build(wordList);  
             //若最终的结果单词都不在词典中，返回空的答案  
             if (!dic.contains(endWord)) {  
                 return ans;  
             }  
             //若能找到从begin到end的路径  
             if (bfs(beginWord, endWord)) {  
                 dfs(endWord, beginWord);  
             }  
             return ans;  
         }  
   
         public static void build(List<String> wordList) {  
             dic = new HashSet<>(wordList);  
             graph.clear();  
             curLevel.clear();  
             nextLevel.clear();  
             ans.clear();  
         }  
   
         public static boolean bfs(String beginWord, String endWord) {  
             boolean find = false;  
             curLevel.add(beginWord);  
             //宽度优先遍历，寻找路径，找到的只要保证每层的单词没有一样的，就必定是最短的  
             while (!curLevel.isEmpty()) {  
                 //移除已经出现遍历过的单词  
                 dic.removeAll(curLevel);  
                 //对当前层的每个单词寻找改变一个字母后，在词典中可以找到的单词，注意反向建图  
                 for (String world : curLevel) {  
                     char[] w = world.toCharArray();  
                     //这里有个小技巧，对于每个单词由于1 <= beginWord.length <= 5  
                     //所以我们让每个位置的字母分别在26个小写字母中尝试，而不是与词典中的单词比较判定，从而减少计算量  
                     for (int i = 0; i < w.length; i++) {  
                         char old = w[i];  
                         for (char j = 'a'; j <= 'z'; j++) {  
                             w[i] = j;  
                             String str = String.valueOf(w);  
                             if (dic.contains(str) && !str.equals(world)) {  
                                 if (str.equals(endWord)) {  
                                     find = true;  
                                 }  
                                 graph.putIfAbsent(str, new ArrayList<>());  
                                 //反向建图，很关键  
                                 graph.get(str).add(world);  
                                 nextLevel.add(str);  
                             }  
                         }  
                         w[i] = old;  
                     }  
                 }  
                 //如果在这一层找到了目标，则最短路径已经出现了，可以直接返回结果了，不用再继续向下找  
                 if (find) {  
                     return true;  
                 } else {  
                     HashSet<String> temp = curLevel;  
                     curLevel = nextLevel;  
                     nextLevel = temp;  
                     nextLevel.clear();  
                 }  
   
             }  
             return false;  
         }  
   
         //由于我们已经反向建图，现在开始从后往前寻找路径  
         public static void dfs(String endWord, String beginWord) {  
             path.addFirst(endWord);  
             if (endWord.equals(beginWord)) {  
                 ans.add(new ArrayList<>(path));  
             } else if (graph.containsKey(endWord)) {  
                 for (String next : graph.get(endWord)) {  
                     dfs(next, beginWord);  
                 }  
             }  
             //递归状态复原  
             path.removeFirst();  
         }  
     }  
 }

参考资料